题目内容
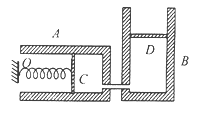
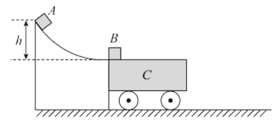
【题目】如图所示,光滑水平地面上有一上表面粗糙且水平、质量为![]() 的小车
的小车![]() 。小车
。小车![]() 与一固定在地面上的光滑圆弧底端等高且平滑相接。将质量为
与一固定在地面上的光滑圆弧底端等高且平滑相接。将质量为![]() 的滑块
的滑块![]() 置于小车
置于小车![]() 的最左端。现有一质量为
的最左端。现有一质量为![]() 的滑块
的滑块![]() 从距离小车的水平面高度为
从距离小车的水平面高度为![]() 处的光滑轨道由静止下滑。滑块
处的光滑轨道由静止下滑。滑块![]() 与
与![]() 碰撞后立即粘在一起运动,最终没有滑落小车。整个过程中滑块
碰撞后立即粘在一起运动,最终没有滑落小车。整个过程中滑块![]() 和
和![]() 都可以视为质点。滑块
都可以视为质点。滑块![]() 和
和![]() 与小车
与小车![]() 之间的动摩擦因数均为
之间的动摩擦因数均为![]() ,取
,取![]() ,求:
,求:
(1)滑块![]() 和
和![]() 粘在一起后和小车
粘在一起后和小车![]() 相对运动过程中各自加速度的大小?
相对运动过程中各自加速度的大小?
(2)若从![]() 碰撞时开始计时,则
碰撞时开始计时,则![]() 时间内,滑块
时间内,滑块![]() 与小车
与小车![]() 因摩擦产生的热量
因摩擦产生的热量![]() 为多少?
为多少?
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)滑块![]() 和
和![]() 粘在一起后,滑块
粘在一起后,滑块![]() 和小车
和小车![]() 都向右运动,设它们的加速度分别为
都向右运动,设它们的加速度分别为![]() 和
和![]() 由牛顿第二定律可得
由牛顿第二定律可得
滑块![]() :
:
![]() ,
,
得:
![]() ,
,
对小车![]() :
:
![]()
得:
![]() ;
;
(2)设滑块![]() 滑到圆弧底端时的速度为
滑到圆弧底端时的速度为![]() ,由机械能守恒定律可得
,由机械能守恒定律可得
![]() ,
,
设![]() 碰撞后的共同速度为
碰撞后的共同速度为![]() ,由动量守恒定律可得:
,由动量守恒定律可得:
![]() ,
,
设在![]() 时间内,滑块
时间内,滑块![]() 与小车
与小车![]() 相对运动时间为
相对运动时间为![]() ,由相对静止时速度相等可得
,由相对静止时速度相等可得
![]() ,
,
解得:
![]() ,
,
即1s后物块和小车相对静止向右匀速直线运动,设在相对运动时间![]() 内,滑块
内,滑块![]() 和小车
和小车![]() 的位移分别为
的位移分别为![]() 和
和![]() ,由匀变速直线运动规律可得
,由匀变速直线运动规律可得
![]() ,
,
![]() ,
,
设滑块![]() 与小车
与小车![]() 相对运动的位移为
相对运动的位移为![]() ,则有
,则有
![]() ,
,
![]() 时间内,滑块
时间内,滑块![]() 与小车
与小车![]() 因摩擦产生的热量
因摩擦产生的热量
![]() ,
,
联立解得:
![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目