��Ŀ����
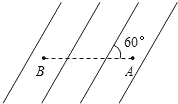
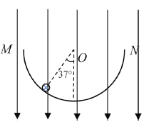
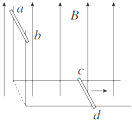
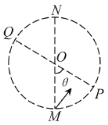
����Ŀ����ͼ��ʾ���뾶ΪR��Բ�������г����˴�ֱֽ���������ǿ�ų���O��Բ�������Բ�ģ�MN��PQ�Ǽн�Ϊ��=![]() ������ֱ����a��b�����������Ӷ���M���ش�ֱ��PQ�ķ������ų������ֱ��P��Q�������뿪���������ӵ�����������˵��һ����ȷ����
������ֱ����a��b�����������Ӷ���M���ش�ֱ��PQ�ķ������ų������ֱ��P��Q�������뿪���������ӵ�����������˵��һ����ȷ����
A.a���Ӵ����磬b���Ӵ�����
B.b�����ڴų����˶���ʱ����a���ӵ�2��
C.��ֻ�ı�b���ӽ���ų�ʱ���ٶȷ����ı��ٶȴ�С����b���Ӿ��Դ�ֱ��MN�ķ�������ų�
D.����a���Ӵ�P�����ų���a���ӿ��ܴ�M���뿪�ų�
���𰸡�AC
��������
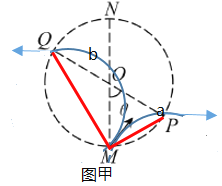
A�������˶��켣��ͼ����ʾ�������ֶ����֪��a���Ӵ����磬b���Ӵ����磬��A��ȷ��
B���������˶��켣�ͼ��ι�ϵ��֪��
![]()
![]()
��
![]()
�����������ڴų��е��˶��뾶��ͬ���ɹ�ʽ
![]()
���ڲ�������ӵ�����������ȣ�������ȷ�������ӵ��˶�ʱ�䣬��B����
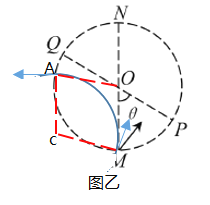
C���ı�b���ӽ���ų�ʱ���ٶȷ����ı��ٶȴ�С���������ӵ��˶��뾶��Բ�δų��뾶��ȣ����ԣ���ͼ�����ı���AOMCΪ���Σ�����ACһ����ֱ���ٶ�һ����ֱMN����C��ȷ��
D������a���Ӵ����磬��P�����ų�������ƫת�����Բ����ܴ�M���������D����
��ѡAC��

��ϰ��ϵ�д�
 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
�����Ŀ