��Ŀ����
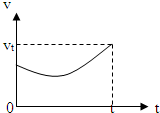
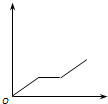
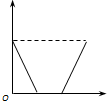
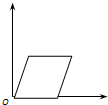
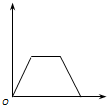
���������ٶ�v����ͨ��ֱ���ϵ�A��B���㣬��ʱΪt���������A�㾲ֹ�����������ٶȴ�СΪa1���ȼ���ֱ���˶�������ijһ����ٶ�vm�����������ٶȴ�СΪa2���ȼ���ֱ���˶�����B��ֹͣ����ʱҲΪt���������������˶��������ж���ȷ���ǣ�������
| A������a1��a2Ϊ��ֵ������ٶ�vm=2v | ||||||
| B������ٶ�vm��Ϊ����ֵ����a1��a2�Ĵ�С�й� | ||||||
| C�����ٶ�a1��a2ֵ������һ���� | ||||||
D�����ٶ�a1��a2��������
|
A������������ͨ��A��B����ʱ��x=vt�����������ȼ��ٺ��ȼ���ͨ��A��B����ʱ������ƽ���ٶȹ�ʽ����λ��x=
t1+
t2=
t�����vm=2v����a1��a2�أ���A��ȷ��B����
C���ȼ����˶���ʱ����ȼ����˶���ʱ��֮��t=
+
=
+
�������ã�
+
=
����C����D��ȷ��
��ѡ��AD��
| vm |
| 2 |
| vm |
| 2 |
| vm |
| 2 |
C���ȼ����˶���ʱ����ȼ����˶���ʱ��֮��t=
| vm |
| a1 |
| vm |
| a2 |
| 2v |
| a1 |
| 2v |
| a2 |
| 1 |
| a1 |
| 1 |
| a2 |
| t |
| 2v |
��ѡ��AD��

��ϰ��ϵ�д�
 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
�����Ŀ