题目内容
17.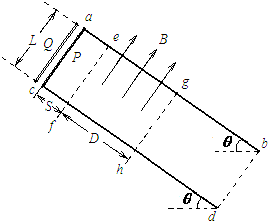 如图所示,电阻不计、间距L=1m、足够长的光滑金属导轨ab、cd与水平面成θ=37°角,导轨平面矩形区域efhg内分布着磁感应强度的大小B=1T,方向垂直导轨平面向上的匀强磁场,边界ef、gh之间的距离D=1.4m.现将质量m=0.1kg、电阻R=$\frac{5}{3}$Ω的导体棒P、Q相隔△t=0.2s先后从导轨顶端由静止自由释放,P、Q在导轨上运动时始终与导轨垂直且接触良好,P进入磁场时恰好匀速运动,Q穿出磁场时速度为2.8m/s.已知重力加速度g=10m/s2,sin37°=0.6,求
如图所示,电阻不计、间距L=1m、足够长的光滑金属导轨ab、cd与水平面成θ=37°角,导轨平面矩形区域efhg内分布着磁感应强度的大小B=1T,方向垂直导轨平面向上的匀强磁场,边界ef、gh之间的距离D=1.4m.现将质量m=0.1kg、电阻R=$\frac{5}{3}$Ω的导体棒P、Q相隔△t=0.2s先后从导轨顶端由静止自由释放,P、Q在导轨上运动时始终与导轨垂直且接触良好,P进入磁场时恰好匀速运动,Q穿出磁场时速度为2.8m/s.已知重力加速度g=10m/s2,sin37°=0.6,求(1)导轨顶端与磁场上边界ef之间的距离S;
(2)从导体棒P释放到Q穿出磁场的过程,回路中产生的焦耳热Q总.
分析 (1)P进入磁场时恰好匀速运动,根据法拉第电磁感应定律、闭合电路欧姆定律、安培力公式推导出P所受的安培力与速度的关系,再由P受力平衡,求出P进入磁场时的速度,最后由牛顿第二定律和运动学公式结合求解S.
(2)分析两棒的运动情况:P进入磁场以速度v1匀速运动△t=0.2s后,Q恰好进入磁场,速度也为v1=2m/s.之后,P、Q以加速度a匀加速运动,P出磁场以后继续以加速度a匀加速运动,而Q在安培力作用下减速运动,直到穿出磁场区域.分段求解回路中产生的热量,从而得到总热量.
解答  解:(1)设P进磁场时的速度为v1,
解:(1)设P进磁场时的速度为v1,
由法拉第电磁感应定律 E=BLv1
由闭合电路欧姆定律 I=$\frac{E}{2R}$
P所受的安培力 F=BIL
P匀速运动,则有 F=mgsinθ
联立解得 v1=2m/s
由牛顿第二定律 a=gsinθ
由运动学公式 S=$\frac{{v}_{1}^{2}}{2a}$
解得 S=$\frac{1}{3}$m≈0.33m
(2)P进入磁场以速度v1匀速运动△t=0.2s后,Q恰好进入磁场,速度也为v1=2m/s.之后,P、Q以加速度a匀加速运动,P出磁场以后继续以加速度a匀加速运动,而Q在安培力作用下减速运动,直到穿出磁场区域.
P在磁场中匀速运动的位移 x1=v1t
此过程回路产生的焦耳热 Q1=mgx1sinθ
P、Q一起匀加速运动的位移 x2=D-x1
设P刚好出磁场时,P、Q的速度为v,由运动学公式
v2-v12=2ax2
解得 v=4m/s
Q出磁场时的速度为v2=2.8m/s,运动的位移 x3=x1.
Q减速运动过程中回路产生的焦耳热
Q2=mgx3sinθ+$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{v}_{2}^{2}$
所以,全过程回路中的焦耳热为Q总=Q1+Q2=0.888J
答:
(1)导轨顶端与磁场上边界ef之间的距离S为0.33m;
(2)从导体棒P释放到Q穿出磁场的过程,回路中产生的焦耳热Q总为0.888J.
点评 本题考查电磁感应现象的动力学与能量问题.关键要正确分析导体棒的运动情况,确定其受力情况,同时要抓住两个导体棒之间的关系,比较位移关系等分析.

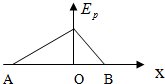 如图所示,空间存在着沿x轴方向的静电场,A、O、B为x轴上的点,图中的折线表示的是一带正电粒子沿x轴在A、B两点间运动时,其电势能EP随x的变化情况.若$\overline{AO}$>$\overline{OB}$,则下列判断正确的是( )
如图所示,空间存在着沿x轴方向的静电场,A、O、B为x轴上的点,图中的折线表示的是一带正电粒子沿x轴在A、B两点间运动时,其电势能EP随x的变化情况.若$\overline{AO}$>$\overline{OB}$,则下列判断正确的是( )| A. | A、B两点的电势一定相等 | |
| B. | 粒子从A向O运动过程中所受电场力均匀增大 | |
| C. | A、O间的电场强度大于O、B间的电场强度 | |
| D. | 若将一带负电的粒子从A点由静止释放,则当粒子运动到O点时动能最大 |
 一半径为R的半球面均匀带有负电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{KQ}{2{R}^{2}}$.把半球面分为表面积相等的左、右两部分,如图所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E1、E2.则( )
一半径为R的半球面均匀带有负电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{KQ}{2{R}^{2}}$.把半球面分为表面积相等的左、右两部分,如图所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E1、E2.则( )| A. | E1<$\frac{kQ}{4{R}^{2}}$ | |
| B. | E2=$\frac{kQ}{4{R}^{2}}$ | |
| C. | 电荷Q在球心O处产生的场强方向垂直于底面向下 | |
| D. | 电荷Q在球心O处产生的场强方向垂直于底面向上 |
| A. | 在定义加速度,电场强度,电容器的电容等物理量时采用了类比法 | |
| B. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| C. | 在用实验探究加速度、力和质量三者之间关系时,应用了控制变量法 | |
| D. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
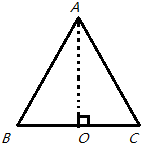 在光滑绝缘的水平面上有边长为L的等边三角形ABC,如图所示,在B,C位置上放有等量同种正电荷,在A点放一带负电的小球,让小球沿BC边的垂直平分线AO运动,则下列说法正确的是( )
在光滑绝缘的水平面上有边长为L的等边三角形ABC,如图所示,在B,C位置上放有等量同种正电荷,在A点放一带负电的小球,让小球沿BC边的垂直平分线AO运动,则下列说法正确的是( )| A. | 带电小球从A到O,电势能减小 | |
| B. | 从A到O小球所受的电场力一直减小 | |
| C. | 从A到O小球所受的电场力先增大后减小 | |
| D. | 小球经过O点时速度为零 |
 如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )
如图为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石子,已知AO=40m,g取10m/s2.下列说法正确的是( )| A. | 若石块不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越大 | |
| B. | 若石块不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越小 | |
| C. | 若石块能落入水中,则v0越大,落水时速度方向与水平面的夹角越大 | |
| D. | 若v0=18m/s,则石块可以落入水中 |
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 理想气体绝热压缩内能会增大 | |
| C. | 理想气体等温膨胀内能会减小 | |
| D. | 热量不可以从低温物体传到高温物体 |
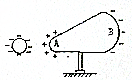 把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )
把一个架在绝缘支座上的导体放在负电荷形成的电场中,导体处于静电平衡时,导体表面上感应电荷的分布如图所示,这时导体( )| A. | A端的电势比B端的电势高 | |
| B. | A端的电荷比B端的电荷密集 | |
| C. | A端额电势可能比B端的电势高,也可能比B端的电势低 | |
| D. | A端的电势与B端的电势相等 |