题目内容
4.A、B两小球分别带9Q和-3Q的电荷,固定在相距为L的位置上,现有一电荷量为Q的小球C,问将它放在什么位置受到的静电力为零?分析 根据题意可知,要是第三个电荷所受静电力为零,则该处的场强应该为零,由点电荷电场强度的叠加为零,从而确定具体位置.
解答 解:根据同种电荷相吸,异种电荷相斥,因此小球C只可能在AB连线的右侧,
设带电荷为Q的小球C,距-3Q位置为r
要使所受的静场力为0,那么该处的电场强度为0,
故有k9Q(L+r)2=k3Qr2
解得:r=√3+12L
答:将它放在B球的右侧,离B√3+12L的位置受到的静电力为零.
点评 本题要掌握点电荷的场强计算公式和场强叠加原理,注意首先根据方向,来大致确定平衡位置是解题的关键.

练习册系列答案
相关题目
12.如图是某物体做直线运动的v-t图象,下列有关物体运动的情况判断正确的是( )


| A. | 2s末物体的加速度大小为5m/s2 | B. | 4s末物体回到出发点 | ||
| C. | 6s末物体的速度最大 | D. | 4s末物体的加速度为零 |
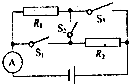 在如图所示的电路中,电源电压保持6V不变,电阻R1的阻值为20Ω.当S2断开,S1、S3闭合时,电流表的示数为0.45A.求:
在如图所示的电路中,电源电压保持6V不变,电阻R1的阻值为20Ω.当S2断开,S1、S3闭合时,电流表的示数为0.45A.求: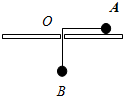 如图所示,光滑的水平圆盘中心O处有一个光滑小孔,用细绳穿过小孔,绳两端各系一个小球A和B,圆盘上的A球随圆盘一起在水平面内做半径为r=10cm的匀速圆周运动,要使B球保持静止状态,(g=10m/s2)求:
如图所示,光滑的水平圆盘中心O处有一个光滑小孔,用细绳穿过小孔,绳两端各系一个小球A和B,圆盘上的A球随圆盘一起在水平面内做半径为r=10cm的匀速圆周运动,要使B球保持静止状态,(g=10m/s2)求:
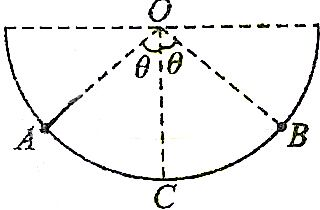 两个半径完全相同的金属小球带有等量的正电荷,放于一竖直半圆环光滑的绝缘面内,静止时两球位置如图所示,已知两球的质量都为m,环的半径为R(小金属球的半径可以忽略),∠AOC=∠BOC=θ,则小球受到的库仑力的大小F=mgtanθ,每个小球上的电荷量Q=2Rsinθ
两个半径完全相同的金属小球带有等量的正电荷,放于一竖直半圆环光滑的绝缘面内,静止时两球位置如图所示,已知两球的质量都为m,环的半径为R(小金属球的半径可以忽略),∠AOC=∠BOC=θ,则小球受到的库仑力的大小F=mgtanθ,每个小球上的电荷量Q=2Rsinθ