题目内容
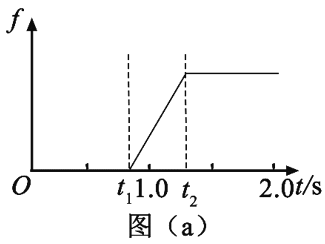
【题目】一质量为m=2000 kg的汽车以某一速度在平直公路上匀速行驶。行驶过程中，司机忽然发现前方100 m处有一警示牌。立即刹车。刹车过程中，汽车所受阻力大小随时间变化可简化为图（a）中的图线。图（a）中，0~t1时间段为从司机发现警示牌到采取措施的反应时间（这段时间内汽车所受阻力已忽略，汽车仍保持匀速行驶），t1=0.8 s；t1~t2时间段为刹车系统的启动时间，t2=1.3 s；从t2时刻开始汽车的刹车系统稳定工作，直至汽车停止，已知从t2时刻开始，汽车第1 s内的位移为24 m，第4 s内的位移为1 m。
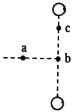
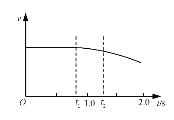
（1）在图（b）中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的v-t图线；
（2）求t2时刻汽车的速度大小及此后的加速度大小；
（3）求刹车前汽车匀速行驶时的速度大小及t1~t2时间内汽车克服阻力做的功；司机发现警示牌到汽车停止，汽车行驶的距离约为多少（以t1~t2时间段始末速度的算术平均值替代这段时间内汽车的平均速度）？
【答案】（1）
（2）
， 28 m/s（3）30 m/s；
；87.5 m
【解析】
解：（1）v-t图像如图所示。
（2）设刹车前汽车匀速行驶时的速度大小为v1，则t1时刻的速度也为v1，t2时刻的速度也为v2，在t2时刻后汽车做匀减速运动，设其加速度大小为a，取Δt=1s，设汽车在t2+n-1Δt内的位移为sn，n=1,2,3,…。
若汽车在t2+3Δt~t2+4Δt时间内未停止，设它在t2+3Δt时刻的速度为v3，在t2+4Δt时刻的速度为v4，由运动学有
①
②
③
联立①②③式，代入已知数据解得
④
这说明在t2+4Δt时刻前，汽车已经停止。因此，①式不成立。
由于在t2+3Δt~t2+4Δt内汽车停止，由运动学公式
⑤
⑥
联立②⑤⑥，代入已知数据解得
，v2=28 m/s⑦
或者
，v2=29.76 m/s⑧
第二种情形下v3小于零，不符合条件，故舍去
（3）设汽车的刹车系统稳定工作时，汽车所受阻力的大小为f1，由牛顿定律有：f1=ma⑨
在t1~t2时间内，阻力对汽车冲量的大小为：
⑩
由动量定理有：
由动能定理，在t1~t2时间内，汽车克服阻力做的功为：
联立⑦⑨⑩式，代入已知数据解得
v1=30 m/s
从司机发现警示牌到汽车停止，汽车行驶的距离s约为
联立⑦，代入已知数据解得
s=87.5 m
