Question

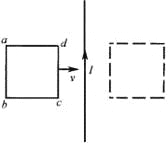
【题目】如图所示，两根足够长的粗糙平行直导轨与水平面成α角放置，两导轨间距为l，轨道上端接一电容为C的电容器．导轨处于匀强磁场中，磁场的磁感应强度大小为B，方向垂直于导轨平面斜向上．一质量为m的金属棒在沿平行斜面的恒力F作用下从静止开始沿斜面向上运动．已知重力加速度大小为g，金属棒与导轨之间的动摩擦因数为μ，忽略所有电阻，求：

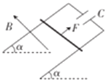
(1)电容器极板上积累的电荷量与金属棒速度大小的关系；

(2)回路中的电流强度大小．

Answer 1

【答案】(1)Q＝CBlv (2)

【解析】

(1)由法拉第电磁感应定律求出感应电动势；再与相结合求出电荷量与速度的关系式．

(2)由动量定理求解加速度大小，再由电流强度的定义式求解电流强度大小．

(1)设金属棒下滑的速度大小为v，则感应电动势为：E＝Blv

平行板电容器两极板之间的电势差为：U＝E

设此时电容器极板上积累的电荷量为Q，按定义有：

得：Q＝CBlv

(2)设导体棒运动过程中经过t时间的速度为v，

根据动量定理可得：Ft-μmgcosαt-mgsinαt-BIlt＝mv﹣0，

根据电荷量的计算公式可得：Q＝It＝CBlv

解得:

可见导体棒做匀加速直线运动，通过导体棒的电流强度为：