Question

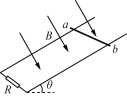
【题目】如图所示的气缸放在水平面上，其横截面积为S=1×10-3m2，质量为m=2kg的活塞将一定质量的理想气体封闭在气缸中，活塞被锁定。活塞距离气缸底部的距离为L1=12cm，气体的温度为T1=300K、压强为P1=1.5×105Pa。已知外界大气压强恒为P0=1.0×105Pa、重力加速度为g=10 m/s2，不计摩擦。求：

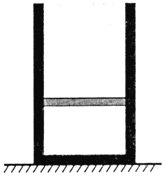
(i)先将封闭气体的温度缓慢升高到T2=400K，然后解除锁定，当活塞再次平衡时，封闭气体的温度为T3=360K，则活塞到气缸底部的距离L3为多少？

(ii)保持封闭气体的温度T3=360K不变，活塞处于解除锁定的状态，现使整个装置竖直向上做匀加速直线运动，若使活塞到气缸底部的距离为L4=16cm，则装置的加速度应为多大？

Answer 1

【答案】(i)＝18cm (ii)a＝7.5m/s2

【解析】

(1)）根据将封闭气体的温度缓慢升高到T2=400K，当活塞再次平衡时，封闭气体的温度为T3=360K可知，根据气体的等容变化和理想气体方程列方程求解；

(2) 根据整个装置竖直向上做匀加速直线运动可知，由牛顿第二定律列方程求解。

(i)由题意知，气体等容变化

解得：

当再次平衡时，活塞受力平衡，故封闭气体压强为

根据理想气体状态方程有

即

解得L3＝18cm；

(i) 由题意知，气体等温变化：

解得：

应向上做匀加速直线运动，对活塞，由牛顿第二定律得：

解得a＝7.5m/s2。