题目内容
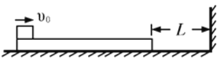
【题目】如图，一质量为m=1kg的木板静止在光滑水平地面上。开始时，木板右端与墙相距L=0.08m；质量为m=1kg的小物块以初速度v0=2m/s滑上木板左端。木板长度可保证物块在运动过程中不与墙接触。物块与木板之间的动摩擦因数为μ=0.1。木板与墙的碰撞是完全弹性的。取g=10m/s2，求：
(1)从物块滑上木板到木板与墙第一次碰撞经过的时间及第一次碰撞前瞬间小物块的速度；
(2)从物块滑上木板到两者达到共同速度时，木板与墙碰撞的次数及所用的时间；
(3)达到共同速度时木板右端与墙之间的距离。
【答案】(1)0.4s；1.6m/s；(2)3；1.8s；(3)0.06m
【解析】
（1）物块滑上木板后，在摩擦力作用下，木板从静止开始做匀加速运动。设木板加速度为a，经历时间T后与墙第一次碰撞，碰撞时的速度为v1，则有
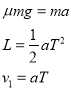
联立解得
物块在木板上滑动过程中，取向右为正方向，根据动量守恒定律有
解得
（2）在物块与木板两者达到共同速度前，在每两次碰撞之间，木板受到物块对它的摩擦力作用而做加速度恒定的运动，因而木板与墙相碰后将返回至初态，所用时间为T。
设在物块与木板两者达到共同速度v前木板共经历n次碰撞，则有
式中△t是碰撞n次后木板从起始位置至达到共同速度时所需要的时间。
由于最终两个物体一起以相同的速度匀速前进，故上式可改写为：
由于木板的速率只能位于0到v1之间，故有
又
解得
，
由于n是整数，故n=2
由于速度相同后还要再一起与墙壁碰撞一次，故一共碰撞3次；
从开始到物块与木板两者达到共同速度所用的时间为
即从物块滑上木板到两者达到共同速度时，木板与墙共发生3次碰撞，所用的时间为1.8s。
（3）物块与木板达到共同速度时，木板与墙之间的距离为
代入数据解得
即达到共同速度时木板右端与墙之间的距离为0.06m。
