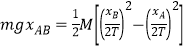Question

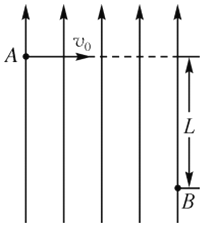
【题目】如图所示，A、E分别是斜面的顶端和底端，B、C、D 是斜面上的三个点，且AB=BC=CD=DE。从 A 点以不同的水平速度向左抛出两个小球（不计空气阻力），球 1 落在 B 点，球 2 落在 E点。两球从抛出到落在斜面上的运动过程中，下列说法正确的是（　　）

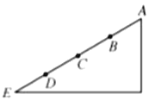
A.球1和球2 运动的时间之比为1∶2B.球1和球2 抛出时初速度大小之比为1∶4

C.球1和球2 落点速度方向相同D.球1和球2落点速度大小之比为1∶4

Answer 1

【答案】AC

【解析】

A．两小球做平抛运动，落到斜面上，竖直方向上做自由落体运动，运动时间

竖直位移之比为1：4，则运动时间之比为1：2，故A正确；
B．设斜面倾角为θ，根据平抛运动的规律结合几何关系可知，斜面的倾角等于位移与水平方向的夹角，位移与水平方向夹角的正切值

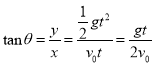
解得初速度为

则球1和球2抛出时初速度大小之比为1：2，故B错误；
C．根据平抛运动的规律可知，速度与水平方向夹角φ的正切值等于位移与水平方向夹角θ的正切值的二倍，tanφ=2tanθ，位移与水平方向夹角θ相同，则两小球落到斜面上速度方向相同，故C正确；
D．若速度与水平方向夹角φ，则小球落点速度

则球1和球2落点速度大小之比为1：2，故D错误。
故选AC。