题目内容
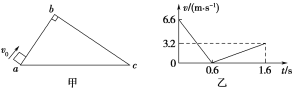
【题目】如图甲所示,以两虚线M、N为边界,中间存在平行纸面且与边界垂直的水平电场,M、N间电压UMN的变化图象如图乙所示,电压的最大值为U0、周期为T0;M、N两侧为相同的匀强磁场区域Ⅰ、Ⅱ,磁场方向垂直纸面向里,磁感应强度为B.t=0时,将一带正电的粒子从边界线M上的A处由静止释放,经电场加速后进入磁场,粒子在磁场中做圆周运动的周期也为T0。两虚线M、N间宽度很小,粒子在其间的运动时间不计,也不考虑粒子所受的重力.
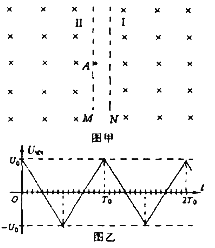
(1)求该粒子的比荷;
(2)求粒子第1次和第2次从右向左经边界线N离开磁场区域Ⅰ时两位置间的距离Δd;
(3)若粒子的质量增加![]() ,电荷量不变,t=0时,将其在A处由静止释放,求t=2T0时粒子的速度。
,电荷量不变,t=0时,将其在A处由静止释放,求t=2T0时粒子的速度。
【答案】(1)![]() (2)
(2)![]() (3)
(3)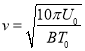
【解析】(1)根据![]() ,周期
,周期![]() 得
得![]() .
.
解得![]() .
.
(2)第1次自右向左穿过边界线N后再加速一次进入磁场区域Ⅱ时的速度为v1,共被加速2次.
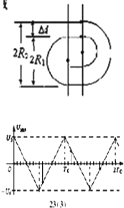
2qU0=![]() mv12,解得
mv12,解得![]() .
.
第2次自右向左穿过边界N时被加速3次,速度为v2
3qU0=![]() mv22,解得
mv22,解得![]() .
.
因为![]()
所以![]() .
.
(3)因为周期![]()
粒子的质量增加![]() ,则周期为T=
,则周期为T=![]() T0
T0
增加△T=![]() T
T
每半个周期为![]() ,增加了
,增加了![]() T0
T0
从t=0开始到t=2T0为止的时间内,粒子共加速了4次,电压分别为:U0、![]() U0、
U0、![]() U0、
U0、![]() U0
U0
由动能定理得, ![]()
解得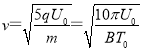

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目