题目内容
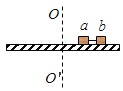
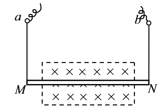
【题目】如图所示，质量均为m的物块A、B放在水平圆盘上，它们到转轴的距离分别为r、2r，圆盘做匀速圆周运动。当转动的角速度为ω时，其中一个物块刚好要滑动，不计圆盘和中心轴的质量，不计物块的大小，两物块与圆盘间的动摩擦因数相同，重力加速度为g，最大静摩擦力等于滑动摩擦力，求：
(1)物块与圆盘间的动摩擦因数为多少；
(2)用细线将A、B两物块连接，细线刚好拉直，圆盘由静止开始逐渐增大转动的角速度，当两物块刚好要滑动时，外力对转轴做的功为多少。
【答案】（1）
（2）
【解析】
(1) 由分析可知，物块离转轴的距离越大，越容易滑动，因此最先滑动的是物块B。根据牛顿第二定律
解得：
(2) 当两物块刚好要滑动时，设转动的角速度为ω1．对物块A研究有：
对物块B研究有：
解得：
则物块A的线速度大小为：
物块B的线速度大小为：
根据功能关系可得，外力做的功为：
练习册系列答案
手拉手全优练考卷系列答案
相关题目
