题目内容
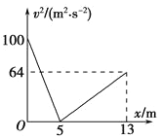
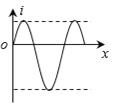
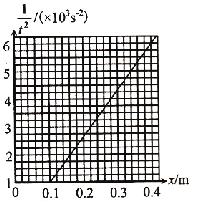
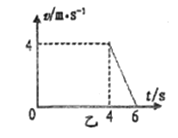
【题目】在倾角θ=370的固定粗糙绝缘斜面上有一质量m=0.1kg,带量为q=+1.15×10-4C的小物块,处于如图甲所示的水平方向匀强电场中,t=0时刻物块以某一初速度从斜面上A点沿斜面下滑,在t=4s时滑到水平面上,此时撤去电场,在这以后的一段时间内物块运动的速度随时间变化关系v-t图象如图乙所示。已知A点到斜面底端的距离x=18m,物块与各接触面之间的动摩擦因数相同,不考虑转角处机械能损失,g=10m/s2,sin370=0.6,cos370=0.8。求:

(1)物块在A点的速度;
(2)水平匀强电场的场强E(保留2位有效数字)。
【答案】(1)5m/s(2)E=1.0×104N/C
【解析】
根据平均速度公式即可求出物块在A点的速度;根据加速度定义式求出加速度,再结合牛顿第二定律即可求出场强。
(1)设物体在斜面上运动的加速度大小为a 1,方向沿斜面向上,则
0--4s内物体平均速度:![]()
物块在A点的速度为vA ,有 ![]()
解得:vA=5m/s
(2)根据:![]()
设物块与接触面间的摩擦因数为![]() ,物块在水平面上运动时,有
,物块在水平面上运动时,有![]()
由图线可知:![]()
解得:![]()
物块在斜面上运动时,设受的摩擦力为f,则
![]()
联立解得:E=1.0×104N/C

练习册系列答案
相关题目