题目内容
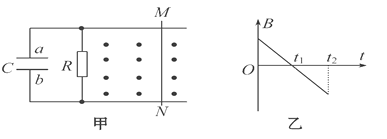
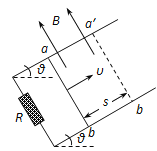
【题目】如图甲所示，两根完全相同的光滑平行导轨固定，每根导轨均由两段与水平成θ=30°的长直导轨和--段圆弧导轨平滑连接而成，导轨两端均连接电阻，阻值
=2Ω，导轨闻距L=0.6m。在右侧导轨所在斜面的矩形区域
内分布有垂直斜面向上的磁场，磁场上下边界
、
.的距离d=0.2m，磁感应强度大小随时间的变化规律如图乙所示。t=0时刻，在右侧导轨斜面上与距离s=0.1m处。有一根阻值r=2Ω的金属棒ab垂直于导轨由静止释放，恰好独立匀速通过整个磁场区域，取重力加速度g=10m/s，导轨电阻不计。求；
(1)ab在磁场中运动的速度大小v；
(2)在
=0.1s时刻和
=0.25s时刻电阻
的电功率之比
(3)电阻
产生的总热量
.
【答案】(1)
；(2)
(3)Q=0.01J.
【解析】（1）由mgs·sinθ=
mv2
得v=1m/s
（2）棒从释放到运动至M1P1的时间
在t1＝0.1 s时，棒还没进入磁场，有
此时，R2与金属棒并联后再与R1串联
R总＝3 Ω
由图乙可知，t=0.2s后磁场保持不变，ab经过磁场的时间
故在t2＝0.25 s时ab还在磁场中运动，电动势E2＝BLv=0.6V
此时R1与R2并联，R总=3Ω，得R1两端电压U1′＝0.2V
电功率
，故在t1＝0.1 s和t2＝0.25 s时刻电阻R1的电功率比值
（3）设ab的质量为m，ab在磁场中运动时，通过ab的电流
ab受到的安培力FA＝BIL
又mgsinθ= BIL
解得m=0.024kg
在t=0～0.2s时间里，R2两端的电压U2=0.2V，产生的热量
ab最终将在M2P2下方的轨道区域内往返运动，到M2P2处的速度为零，由功能关系可得在t=0.2s后，整个电路最终产生的热量Q=mgdsinθ+mv2=0.036J
由电路关系可得R2产生的热量Q2=
Q=0.006J
故R2产生的总热量Q总= Q1+ Q2=0.01 J
