题目内容
5.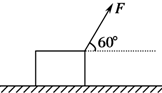 如图所示,在光滑的水平面上放着一个质量为10kg的木箱,拉力F与水平方向成60°角,F=4N,木箱从静止开始运动,4s末拉力的瞬时功率为( )
如图所示,在光滑的水平面上放着一个质量为10kg的木箱,拉力F与水平方向成60°角,F=4N,木箱从静止开始运动,4s末拉力的瞬时功率为( )| A. | 0.8 W | B. | 1.6 W | C. | 3.2 W | D. | 6.4 W |
分析 根据牛顿第二定律求出木箱的加速度,结合速度时间公式求出4s末的速度,通过P=Fvcosθ求出拉力的功率.
解答 解:根据牛顿第二定律得加速度为:
a=$\frac{Fcos60°}{m}=\frac{4×\frac{1}{2}}{10}=0.2m/{s}^{2}$
则4s末的速度为:
v=at=0.2×4m/s=0.8m/s,
则拉力的功率为:
P=Fvcos60°=4×0.8×$\frac{1}{2}$W=1.6W.
故B正确,A、C、D错误.
故选:B.
点评 本题考查了瞬时功率、牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁,知道瞬时功率和平均功率的区别,以及掌握它们的求法.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
6. 如图所示,质量为m的木块放在倾角为α的斜面上于斜面一起水平向左匀速运动,则木块:( )
如图所示,质量为m的木块放在倾角为α的斜面上于斜面一起水平向左匀速运动,则木块:( )
 如图所示,质量为m的木块放在倾角为α的斜面上于斜面一起水平向左匀速运动,则木块:( )
如图所示,质量为m的木块放在倾角为α的斜面上于斜面一起水平向左匀速运动,则木块:( )| A. | 所受的支持力大小为mgcosα | B. | 所受的支持力对木块不做功 | ||
| C. | 所受的摩擦力对木块做负功 | D. | 机械能将逐渐增大 |
13.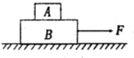 如图所示,一块长木板B放在光滑的水平面上,再在B上放一物体A,现以恒定的外力拉B,A、B发生相对滑动,A、B都向前移动一段距离,在此过程中( )
如图所示,一块长木板B放在光滑的水平面上,再在B上放一物体A,现以恒定的外力拉B,A、B发生相对滑动,A、B都向前移动一段距离,在此过程中( )
 如图所示,一块长木板B放在光滑的水平面上,再在B上放一物体A,现以恒定的外力拉B,A、B发生相对滑动,A、B都向前移动一段距离,在此过程中( )
如图所示,一块长木板B放在光滑的水平面上,再在B上放一物体A,现以恒定的外力拉B,A、B发生相对滑动,A、B都向前移动一段距离,在此过程中( )| A. | 外力F做的功等于A和B动能的增加 | |
| B. | B对A的摩擦力所做的功等于A的动能增量 | |
| C. | A对B的摩擦力所做的功等于B对A的摩擦力所做的功 | |
| D. | 外力F对B做的功等于B的动能的增量与B克服摩擦力所做的功之和 |
20. 理想变压器的原、副线圈匝数比n1:n2=10:1,只有一个副线圈,原线圈两端接交流电源,已知电阻R=5Ω,电压表V的读数为100V,则( )
理想变压器的原、副线圈匝数比n1:n2=10:1,只有一个副线圈,原线圈两端接交流电源,已知电阻R=5Ω,电压表V的读数为100V,则( )
 理想变压器的原、副线圈匝数比n1:n2=10:1,只有一个副线圈,原线圈两端接交流电源,已知电阻R=5Ω,电压表V的读数为100V,则( )
理想变压器的原、副线圈匝数比n1:n2=10:1,只有一个副线圈,原线圈两端接交流电源,已知电阻R=5Ω,电压表V的读数为100V,则( )| A. | 原、副线圈中电流频率之比f1:f2=10:1 | |
| B. | 电流表A2的读数2A | |
| C. | 电流表A1的读数0.2A | |
| D. | 变压器的输入功率为200W |
10.关于做功和物体动能变化的关系,不正确的是( )
| A. | 合外力对物体做正功时,物体的动能一定增加 | |
| B. | 合外力对物体做正功时,物体的动能可能减少 | |
| C. | 外力对物体做功的代数和等于物体的末动能与初动能之差 | |
| D. | 合外力对物体做的功等于物体的末动能与初动能之差 |
15.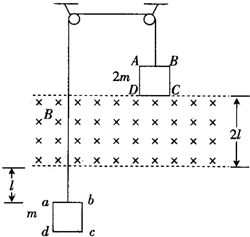 如图所示,同一竖直面内的正方形导线框ABCD、abcd的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时,ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,则( )
如图所示,同一竖直面内的正方形导线框ABCD、abcd的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时,ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,则( )
 如图所示,同一竖直面内的正方形导线框ABCD、abcd的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时,ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,则( )
如图所示,同一竖直面内的正方形导线框ABCD、abcd的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时,ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,则( )| A. | 系统匀速运动的速度大小为$\frac{mgR}{{2{B^2}{l^2}}}$ | |
| B. | 从开始运动至ABCD全部进入磁场的过程中.两线框组成的系统克服安培力做的功为mgl-$\frac{{3{m^3}{g^2}{R^2}}}{{2{B^4}{l^4}}}$ | |
| C. | 两线框从开始运动至等高的过程中,所产生的总焦耳热为2mgl-$\frac{{3{m^3}{g^2}{R^2}}}{{4{B^4}{l^4}}}$ | |
| D. | 线框abcd通过磁场的时间为$\frac{{3{B^2}{l^3}}}{mgR}$ |
 如图所示,足够长的平行光滑金属导轨水平放置,宽度L=0.4m,一端连接R=1Ω的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度B=1T.导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接解良好.导轨和导体棒的电阻均可忽略不计.在平行于导轨的拉力F作用下,导体棒沿导轨向右匀速运动,速度v=5m/s.求:
如图所示,足够长的平行光滑金属导轨水平放置,宽度L=0.4m,一端连接R=1Ω的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度B=1T.导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接解良好.导轨和导体棒的电阻均可忽略不计.在平行于导轨的拉力F作用下,导体棒沿导轨向右匀速运动,速度v=5m/s.求: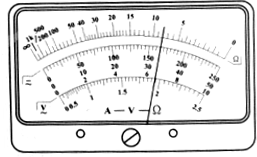 如图所示是学生实验用的多用电表刻度盘,当选用量程为50V的直流电压档测量电压时,表针指于图示位置,则所测电压为33.0V,若选用倍率为“×100”的电阻档测电阻时.表针也指于同一位置,则所测电阻的阻值为800Ω.
如图所示是学生实验用的多用电表刻度盘,当选用量程为50V的直流电压档测量电压时,表针指于图示位置,则所测电压为33.0V,若选用倍率为“×100”的电阻档测电阻时.表针也指于同一位置,则所测电阻的阻值为800Ω. 如图所示,甲乙两物体自同一水平线上同时开始运动,甲沿顺时针方向做匀速圆周运动,圆半径为R,乙做自由落体运动,当乙下落至A点时(A与圆周的最低点等高),甲恰好第一次运动到最高点B,求
如图所示,甲乙两物体自同一水平线上同时开始运动,甲沿顺时针方向做匀速圆周运动,圆半径为R,乙做自由落体运动,当乙下落至A点时(A与圆周的最低点等高),甲恰好第一次运动到最高点B,求