题目内容
15.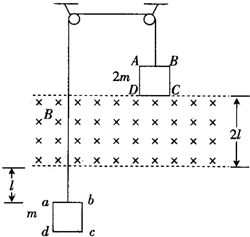 如图所示,同一竖直面内的正方形导线框ABCD、abcd的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时,ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,则( )
如图所示,同一竖直面内的正方形导线框ABCD、abcd的边长均为l,电阻均为R,质量分别为2m和m.它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时,ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,则( )| A. | 系统匀速运动的速度大小为$\frac{mgR}{{2{B^2}{l^2}}}$ | |
| B. | 从开始运动至ABCD全部进入磁场的过程中.两线框组成的系统克服安培力做的功为mgl-$\frac{{3{m^3}{g^2}{R^2}}}{{2{B^4}{l^4}}}$ | |
| C. | 两线框从开始运动至等高的过程中,所产生的总焦耳热为2mgl-$\frac{{3{m^3}{g^2}{R^2}}}{{4{B^4}{l^4}}}$ | |
| D. | 线框abcd通过磁场的时间为$\frac{{3{B^2}{l^3}}}{mgR}$ |
分析 当ABCD刚全部进入磁场时,系统开始做匀速运动,分别对两线框列平衡方程,可得abcd框安培力大小,继而求得感应电流大小,根据欧姆定律和法拉第电磁感应定律可得系统匀速运动的速度大小,即可求得线框abcd通过磁场的时间.
当左、右两线框分别向上、向下运动2l的距离时,两线框等高,根据能量守恒得系统机械能的减少等于产生的总焦耳热.
根据功能关系求解两线框组成的系统克服安培力做的功.
解答 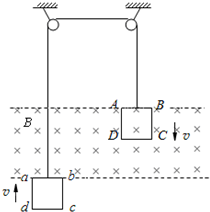 解:AD、如图所示,设两线框刚匀速运动的速度为v,此时轻绳上的张力为T,则对ABCD有:T=2mg…①
解:AD、如图所示,设两线框刚匀速运动的速度为v,此时轻绳上的张力为T,则对ABCD有:T=2mg…①
对abcd有:T=mg+BIl…②
I=$\frac{E}{R}$…③
E=Blv…④
则:v=${\frac{mgR}{{B}^{2}{l}^{2}}}^{\;}$…⑤
线框abcd通过磁场时以速度v匀速运动,设线框abcd通过磁场的时间为t,则:t=$\frac{3l}{v}$=$\frac{3{B}^{2}{l}^{3}}{mgR}$…⑥,故A错误,D正确.
B、从开始运动至ABCD全部进入磁场的过程中,两线框组成的系统克服安培力做的功为W,则有:W+$\frac{1}{2}•$3mv2=2mgl-mgl
可得 W=mgl-$\frac{3{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{l}^{4}}$.故B正确.
C、设两线框从开始运动至等高的过程中所产生的焦耳热为Q,当左、右两线框分别向上、向下运动2l的距离时,两线框等高,对这一过程,由能量守恒定律有:
4mgl=2mgl+$\frac{1}{2}•$3mv2+Q…⑦
解⑤⑥得:Q=2mgl-$\frac{3{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{l}^{4}}$.故C错误.
故选:BD.
点评 本题是电磁感应中的力学问题,安培力的计算和分析能量如何转化是解题关键,要加强训练,熟练掌握法拉第定律、欧姆定律、安培力等等基础知识,提高解题能力.

 名校课堂系列答案
名校课堂系列答案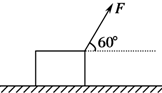 如图所示,在光滑的水平面上放着一个质量为10kg的木箱,拉力F与水平方向成60°角,F=4N,木箱从静止开始运动,4s末拉力的瞬时功率为( )
如图所示,在光滑的水平面上放着一个质量为10kg的木箱,拉力F与水平方向成60°角,F=4N,木箱从静止开始运动,4s末拉力的瞬时功率为( )| A. | 0.8 W | B. | 1.6 W | C. | 3.2 W | D. | 6.4 W |
| A. | 在核反应堆中,为使快中子减速,在铀棒周围要放“慢化剂”,常用的慢化剂有石墨、重水和普通水 | |
| B. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减少,原子总能量增大 | |
| C. | 当用蓝色光照射某金属表面时有电子逸出,则改用红光照射也一定会有电子逸出 | |
| D. | 核力是弱相互作用的一种表现,在原子核的尺度内,核力比库仑力大得多,其作用范围在1.5×l0-10 m | |
| E. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,原子总能量增加 |
 如图,质量为5kg的物体,在F=20N的水平拉力作用下,沿粗糙水平桌面做匀加速直线运动,已知桌面与物体间的动摩擦因数μ=0.2,取则物体在运动过程中受到的滑动摩擦力和加速度大小分别为( )
如图,质量为5kg的物体,在F=20N的水平拉力作用下,沿粗糙水平桌面做匀加速直线运动,已知桌面与物体间的动摩擦因数μ=0.2,取则物体在运动过程中受到的滑动摩擦力和加速度大小分别为( )| A. | 20N和4m/s2 | B. | 10N和2m/s2 | C. | 30N和6m/s2 | D. | 20N和2m/s2 |
 如图所示,一理想变压器接在正弦交变电源上,变压器原、副线圈匝数比为1:2,A为理想交流电流表,副线圈电路中标有“36V,360W”电动机正常工作,若电动机线圈电阻r=0.6Ω,则( )
如图所示,一理想变压器接在正弦交变电源上,变压器原、副线圈匝数比为1:2,A为理想交流电流表,副线圈电路中标有“36V,360W”电动机正常工作,若电动机线圈电阻r=0.6Ω,则( )| A. | 电流表的示数为5A | |
| B. | 原线圈所加交变电压的有效值为18V | |
| C. | 电动机正常工作时的输出功率为300W | |
| D. | 若在电动机正常工作时,转子突然卡住,则电动机的发热功率为60W |
 如图所示是一定质量理想气体的p-T图线(p为气体压强,T为热力学温度),气体状态从图中A沿直线变化到B的过程中,下列表述正确的是( )
如图所示是一定质量理想气体的p-T图线(p为气体压强,T为热力学温度),气体状态从图中A沿直线变化到B的过程中,下列表述正确的是( )| A. | 气体的体积逐渐变小 | |
| B. | 外界对气体做功使气体内能增加 | |
| C. | 每个气体分子热运动的动能都逐渐增大 | |
| D. | 气体从外界吸收的热量大于气体内能的增加量 |
| A. | 频率是30Hz | B. | 波长是3m | C. | 波速是1m/s | D. | 周期是0.1s |
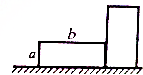 如图所示,质量为$\frac{m}{2}$的均匀长方体木块,边长分别是a和b,平卧在水平地面上,现把它竖起来,人至少要对它做功为$\frac{mgb}{4}$.
如图所示,质量为$\frac{m}{2}$的均匀长方体木块,边长分别是a和b,平卧在水平地面上,现把它竖起来,人至少要对它做功为$\frac{mgb}{4}$.