题目内容
14. 如图所示,甲乙两物体自同一水平线上同时开始运动,甲沿顺时针方向做匀速圆周运动,圆半径为R,乙做自由落体运动,当乙下落至A点时(A与圆周的最低点等高),甲恰好第一次运动到最高点B,求
如图所示,甲乙两物体自同一水平线上同时开始运动,甲沿顺时针方向做匀速圆周运动,圆半径为R,乙做自由落体运动,当乙下落至A点时(A与圆周的最低点等高),甲恰好第一次运动到最高点B,求(1)甲物体做匀速圆周运动的角速度;
(2)甲物体做匀速圆周运动的向心加速度.
分析 (1)根据自由落体运动求出时间,根据等时性求解周期,根据$ω=\frac{2π}{T}$求解角速度;
(2)根据向心加速度定义公式an=ω2R求出向心加速度.
解答 解:(1)设乙下落到A点的时间为t,则对乙满足R=$\frac{1}{2}$gt2,得t=$\sqrt{\frac{2R}{g}}$;
这段时间内甲运动了$\frac{3}{4}$T,即$\frac{3}{4}$T=$\sqrt{\frac{2R}{g}}$
解得:T=$\frac{4}{3}\sqrt{\frac{2R}{g}}$,
则角速度$ω=\frac{2π}{T}=\frac{3π}{2}\sqrt{\frac{g}{2R}}$
(2)向心加速度an=ω2R=$\frac{9}{8}$π2g
答:(1)甲物体做匀速圆周运动的角速度为$\frac{3π}{2}\sqrt{\frac{g}{2R}}$;
(2)甲物体做匀速圆周运动的向心加速度$\frac{9}{8}$π2g.
点评 本题关键根据等时性求出运动的周期,进而求出角速度,然后根据an=ω2R求解向心加速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.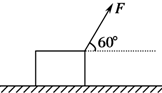 如图所示,在光滑的水平面上放着一个质量为10kg的木箱,拉力F与水平方向成60°角,F=4N,木箱从静止开始运动,4s末拉力的瞬时功率为( )
如图所示,在光滑的水平面上放着一个质量为10kg的木箱,拉力F与水平方向成60°角,F=4N,木箱从静止开始运动,4s末拉力的瞬时功率为( )
 如图所示,在光滑的水平面上放着一个质量为10kg的木箱,拉力F与水平方向成60°角,F=4N,木箱从静止开始运动,4s末拉力的瞬时功率为( )
如图所示,在光滑的水平面上放着一个质量为10kg的木箱,拉力F与水平方向成60°角,F=4N,木箱从静止开始运动,4s末拉力的瞬时功率为( )| A. | 0.8 W | B. | 1.6 W | C. | 3.2 W | D. | 6.4 W |
2.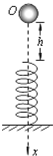 如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
 如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )
如图所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,那么从小球压上弹簧后继续向下运动到最低点的过程中,以下说法正确的是( )| A. | 弹簧的弹性势能先减小后增大 | |
| B. | 球刚接触弹簧时动能最大 | |
| C. | 球所受合力的最大值可能等于重力 | |
| D. | 该过程的某一阶段内,小球的动能增大而小球的机械能减少 |
9.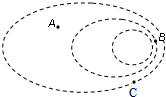 如图所示,虚线为电场中的三个等势面,相邻等势面之间的电势差相等.A、B、C为电场中的三个点,一个带负电的点电荷在A点的电势能大于其在B点的电势能,则下列说法正确的是( )
如图所示,虚线为电场中的三个等势面,相邻等势面之间的电势差相等.A、B、C为电场中的三个点,一个带负电的点电荷在A点的电势能大于其在B点的电势能,则下列说法正确的是( )
 如图所示,虚线为电场中的三个等势面,相邻等势面之间的电势差相等.A、B、C为电场中的三个点,一个带负电的点电荷在A点的电势能大于其在B点的电势能,则下列说法正确的是( )
如图所示,虚线为电场中的三个等势面,相邻等势面之间的电势差相等.A、B、C为电场中的三个点,一个带负电的点电荷在A点的电势能大于其在B点的电势能,则下列说法正确的是( )| A. | A点的电势比B点的低 | |
| B. | A点的电场强度比B点的大 | |
| C. | AC间的电势差大于AB间的电势差 | |
| D. | 沿直线从A运动到B过程中,电场力先做正功后做负功 |
19.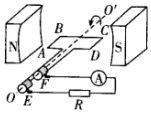 如图所示是小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,线圈的匝数为n、电阻为r,外接电阻为R,其他电阻不计.线圈从图示位置(线圈平面平行于磁场方向)开始转过$\frac{π}{3}$时的感应电流为I.下列说法中正确的是( )
如图所示是小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,线圈的匝数为n、电阻为r,外接电阻为R,其他电阻不计.线圈从图示位置(线圈平面平行于磁场方向)开始转过$\frac{π}{3}$时的感应电流为I.下列说法中正确的是( )
 如图所示是小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,线圈的匝数为n、电阻为r,外接电阻为R,其他电阻不计.线圈从图示位置(线圈平面平行于磁场方向)开始转过$\frac{π}{3}$时的感应电流为I.下列说法中正确的是( )
如图所示是小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,线圈的匝数为n、电阻为r,外接电阻为R,其他电阻不计.线圈从图示位置(线圈平面平行于磁场方向)开始转过$\frac{π}{3}$时的感应电流为I.下列说法中正确的是( )| A. | 电流表的读数为2I | |
| B. | 转动过程中穿过线圈的磁通量的最大值为$\frac{2I(r+R)}{nω}$ | |
| C. | 从图示位置开始转过$\frac{π}{2}$的过程中,通过电阻R的电荷量为$\frac{2I}{ω}$ | |
| D. | 线圈转动一周的过程中,电阻R产生的热量为$\frac{4{I}^{2}πR}{ω}$ |
6.下列关于原子及原子核的说法正确的是( )
| A. | 在核反应堆中,为使快中子减速,在铀棒周围要放“慢化剂”,常用的慢化剂有石墨、重水和普通水 | |
| B. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减少,原子总能量增大 | |
| C. | 当用蓝色光照射某金属表面时有电子逸出,则改用红光照射也一定会有电子逸出 | |
| D. | 核力是弱相互作用的一种表现,在原子核的尺度内,核力比库仑力大得多,其作用范围在1.5×l0-10 m | |
| E. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,原子总能量增加 |
3. 如图,质量为5kg的物体,在F=20N的水平拉力作用下,沿粗糙水平桌面做匀加速直线运动,已知桌面与物体间的动摩擦因数μ=0.2,取则物体在运动过程中受到的滑动摩擦力和加速度大小分别为( )
如图,质量为5kg的物体,在F=20N的水平拉力作用下,沿粗糙水平桌面做匀加速直线运动,已知桌面与物体间的动摩擦因数μ=0.2,取则物体在运动过程中受到的滑动摩擦力和加速度大小分别为( )
 如图,质量为5kg的物体,在F=20N的水平拉力作用下,沿粗糙水平桌面做匀加速直线运动,已知桌面与物体间的动摩擦因数μ=0.2,取则物体在运动过程中受到的滑动摩擦力和加速度大小分别为( )
如图,质量为5kg的物体,在F=20N的水平拉力作用下,沿粗糙水平桌面做匀加速直线运动,已知桌面与物体间的动摩擦因数μ=0.2,取则物体在运动过程中受到的滑动摩擦力和加速度大小分别为( )| A. | 20N和4m/s2 | B. | 10N和2m/s2 | C. | 30N和6m/s2 | D. | 20N和2m/s2 |
4.平静湖面传播着一列水面波(横波),在波的传播方向上有相距3m的甲、乙两个小木块随波上下运动,测得两个小木块每分钟都上下30次,甲在波谷时,乙在波峰,且两木块之间有一个波峰.这列水面波( )
| A. | 频率是30Hz | B. | 波长是3m | C. | 波速是1m/s | D. | 周期是0.1s |
