题目内容
如图所示,半径为0.1 m的轻滑轮,通过绕在其上面的细线与重物相连,若重物由静止开始以2 m/s2的加速度匀加速下落,则当它下落高度为1 m时的瞬时速度是多大?此刻的滑轮转动的角速度是多大?

2 m/s 20 rad/s
【解析】可以依据运动学公式求出重物下落高度为1 m时的瞬时速度,此速度即为滑轮轮缘上的点的圆周运动的线速度,结合线速度与角速度关系式即可解得滑轮转动的角速度.
重物做初速度为零的匀加速直线运动,依运动学公式v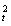 =2as可以求得重物由静止开始下滑1 m时的瞬时速度为vt=
=2as可以求得重物由静止开始下滑1 m时的瞬时速度为vt=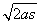 =
=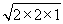 m/s=2 m/s
m/s=2 m/s
与重物相连的细线此刻的速度也等于vt=2 m/s.细线绕在轻滑轮边缘,使滑轮转动,由公式v=rω得,此刻滑轮转动的角速度为ω=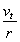 =
=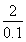 rad/s=20 rad/s
rad/s=20 rad/s
故当重物下落高度为1 m时的瞬时速度是2 m/s,此刻的滑轮转动的角速度是20 rad/s.

练习册系列答案
相关题目
太阳系八大行星公转轨道可近似看做圆轨道,“行星公转周期的平方”与“行星与太阳的平均距离的三次方”成正比.地球与太阳之间平均距离约为1.5亿千米,结合下表可知,火星与太阳之间的平均距离约为( ).
| 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
公转周期(年) | 0.241 | 0.615 | 1.0 | 1.88 | 11.86 | 29.5 |
A.1.2亿千米 B.2.3亿千米
C.4.6亿千米 D.6.9亿千米



