题目内容
16.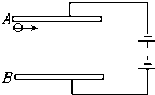 水平放置的平行金属板A、B间的距离为d,两板长度均L,两板间接入电压为U的稳压电源,一电子以v0的水平速度,紧靠板A射入电场,已知电子电量为e,质量为m. 求:
水平放置的平行金属板A、B间的距离为d,两板长度均L,两板间接入电压为U的稳压电源,一电子以v0的水平速度,紧靠板A射入电场,已知电子电量为e,质量为m. 求:(1)两板间的电场强度E的大小和方向;
(2)电子飞出两极板间所用时间和飞出极板时的侧移量.
分析 (1)根据动能定理求出电子通过B点时的速度大小;
(2)电子进入偏转电场后做类平抛运动,根据水平方向上做匀速直线运动,求出运动的时间,结合竖直方向上做匀加速直线运动求出侧移距离.
解答 解:(1)由匀强电场知:E=$\frac{U}{d}$,
方向竖直向上.
(2)电子作类平抛运动有:$\frac{eU}{d}=ma$,
解得:a=$\frac{eU}{md}$
L=v0t
y=$\frac{1}{2}a{t}^{2}$
解之得:$y=\frac{eU{L}^{2}}{2md{v}_{0}{\;}^{2}}$
t=$\frac{L}{{v}_{0}}$
答:(1)两板间的电场强度E的大小为$\frac{U}{d}$,方向竖直向上;
(2)电子飞出两极板间所用时间为$\frac{L}{{v}_{0}}$,飞出极板时的侧移量为$\frac{eU{L}^{2}}{2md{v}_{0}{\;}^{2}}$.
点评 本题考查了带电粒子在电场中的加速和偏转,掌握处理带电粒子在偏转电场中运动的方向,结合牛顿第二定律和运动学公式,抓住等时性进行求解.

练习册系列答案
相关题目
6.如图所示,为某质点的运动的V-t图象,下列有关说法正确的是( )


| A. | 第1s末速度改变方向 | B. | 第2s末位移改变方向 | ||
| C. | 第4s末位移最大 | D. | 第2s末位移最大 |
4.关于摩擦力的说法正确的是( )
| A. | 滑动摩擦力的方向总是与物体的运动方向相反 | |
| B. | 滑动摩擦力总是阻碍物体的运动 | |
| C. | 正压力越大,静摩擦力越大 | |
| D. | 静摩擦力的方向总是与物体的相对运动趋势的方向相反 |
11. 如图所示,从同一位置上以不同的初速v1、v2水平抛出,落到不同的位置,水平位移分别为x1、x2,落地的时间分别为t1、t2,不计空气阻力,则以下关系正确的是( )
如图所示,从同一位置上以不同的初速v1、v2水平抛出,落到不同的位置,水平位移分别为x1、x2,落地的时间分别为t1、t2,不计空气阻力,则以下关系正确的是( )
 如图所示,从同一位置上以不同的初速v1、v2水平抛出,落到不同的位置,水平位移分别为x1、x2,落地的时间分别为t1、t2,不计空气阻力,则以下关系正确的是( )
如图所示,从同一位置上以不同的初速v1、v2水平抛出,落到不同的位置,水平位移分别为x1、x2,落地的时间分别为t1、t2,不计空气阻力,则以下关系正确的是( )| A. | t1<t2 | B. | t1=t2 | C. | v1>v2 | D. | v1<v2 |
5.下列关于位移(矢量)和温度(标量)的说法中,正确的是( )
| A. | 两个运动物体的位移大小均为30 m,则这两个位移一定相同 | |
| B. | 做直线运动的两物体的位移x甲=3 m,x乙=-5 m,则x甲>x乙 | |
| C. | 温度计读数有正也有负,其正、负号表示方向 | |
| D. | 温度计读数的正、负号表示温度的高低,不能表示方向 |
6.一小球从静止开始做匀加速直线运动,在第15s内的位移比第14s内的位移多0.2m,则下列说法正确的是( )
| A. | 小球加速度为0.1m/s2 | B. | 小球第14s的初速度为2.6m/s | ||
| C. | 小球前15s内的平均速度为3.0m/s | D. | 小球第15s内的位移为2.9m |