Question

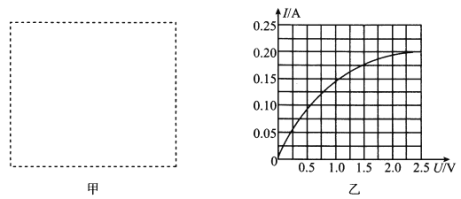
【题目】如图甲所示,足够长的“U”型金属导轨固定在水平面上，金属导轨宽度L=1m，导轨上放有垂直导轨的金属杆P，金属杆质量为m=0.1kg，空间存在磁感应强度B=0.5T，竖直向下的匀强磁场连接在导轨两端的电阻R=3.0Ω，金属杆的电阻r=1.0Ω,其余部分电阻不计某时刻给金属杆一个水平向右的恒力F，金属杆P由静止开始运动，图乙是金属杆P运动过程的图象,导轨与金属杆间的动摩擦因数μ=0.5，在金属杆P运动的过程中,第一个2s内通过金属杆P的电荷量与第二个2s内通过P的电荷量之比为3：5，g取10m/s2,求：

(1)水平恒力F的大小；

(2)求前2s内金属杆P运动的位移大小；

(3)前4s内电阻R上产生的热量．

Answer 1

【答案】（1）0.75N；（2）4.8m；（3）1.8J．

【解析】

（1）由图乙可知金属杆P先作加速度减小的加速运动，2s后做匀速直线运动．当t=2s时，v=4m/s，此时感应电动势

E=Blv

感应电流

安培力

根据牛顿运动定律有

F-F'-μmg=0

解得

F=0.75N

（2）通过金属杆P的电荷量

其中

所以

（x为P的位移）

设第一个2s内金属杆P的位移为x1，第二个2s内P的位移为x2，则

△Φ1=BLx1

△Φ2=BLx=BLvt

由于q1：q2=3：5

联立解得

x2=8m，x1=4.8m．

（3）前4s内由能量守恒得

其中

Qr：QR=r：R=1：3

解得：

QR=1.8J．