��Ŀ����
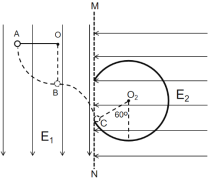
����Ŀ����ͼ��ʾ���ڰ뾶ΪR��Բ�������ڴ�����ǿ�ų����Ÿ�Ӧǿ��ΪB.����ֱ��Բƽ�棨δ��������һȺ����Ϊm�������Ϊ-q����������ͬ����v0��P����ֽƽ������ͬ��������ų��У�����ƫת���ַɳ�������֪���ӵĹ���뾶r���ڴų�����뾶R����������������������˵������ȷ���ǣ� ��

A.���ӷɳ��ų�ʱ�Ķ��ܿ��ܲ����
B.�����ڴų��е��˶��뾶һ�����
C.��PQ��ͬ��������ӷɳ�ʱƫת�����
D.��Q������������ڴų����˶���ʱ���
���𰸡�BD
��������
A���������������Դ������Ӳ�������ֻ�ı����ӵ��˶���������ı����ӵ��ٶȴ�С�������뿪�ų�����ʱ�Ķ�����ȣ���A����
B�������ڴų�����Բ���˶������������ṩ����������ţ�ٵڶ����ɵ�
![]()
��
![]()
�����ӵ�������ͬ���Ⱥ���ͬ���ʰ뾶һ����ͬ����B��ȷ��
CD����Բ�����ʿ�֪���켣Բ��ų�Բ�ཻ�����켣Բ���ҳ����ʱƫ������Ӧ��ʹ�ҳ�ΪPQ������Q��ɳ�������Բ�Ľ��������Ӧ��ʱ��������������Q������ģ�ƫת�����ʱ����һ��������PQ���룬��C����D��ȷ��
��ѡBD��

��ϰ��ϵ�д�
�����Ŀ