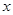题目内容
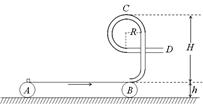
(12分)如图所示,竖直光滑四分之三圆轨道BCD固定在水平面AB上,轨道圆心为O,半径R=1m,轨道最低点与水平面相切于B点,C为轨道最高点,D点与圆心O等高.一质量 的小物块,从水平面上以速度
的小物块,从水平面上以速度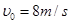 竖直向上抛出,物块从D点进入圆轨道,最终停在A点,物块与水平面间的动摩擦因数
竖直向上抛出,物块从D点进入圆轨道,最终停在A点,物块与水平面间的动摩擦因数 =0.4,取
=0.4,取 .求:
.求:

(1)物块运动到D点时的速度;(可以保留根式)
(2)物块运动到C点时,对轨道的压力大小;
(3)物块从B点运动到A点所用的时间及A、B间的距离.
 的小物块,从水平面上以速度
的小物块,从水平面上以速度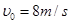 竖直向上抛出,物块从D点进入圆轨道,最终停在A点,物块与水平面间的动摩擦因数
竖直向上抛出,物块从D点进入圆轨道,最终停在A点,物块与水平面间的动摩擦因数 =0.4,取
=0.4,取 .求:
.求:
(1)物块运动到D点时的速度;(可以保留根式)
(2)物块运动到C点时,对轨道的压力大小;
(3)物块从B点运动到A点所用的时间及A、B间的距离.
(1)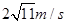 ;(2)
;(2) ;(3)
;(3)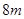 ;2s
;2s
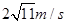 ;(2)
;(2) ;(3)
;(3)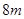 ;2s
;2s试题分析:(1)由公式
 ①
①解得
 ②
②(2)根据机械能守恒定律
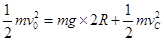 ③
③C点,由牛顿第二定律
 ④
④F=14N ⑤
由牛顿第三定律,物块对轨道的压力
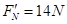 ⑥
⑥(3)由机械能守恒定律知,物体到B点的速度

由动能定理
 ⑦
⑦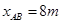 ⑧
⑧由牛顿第二定律
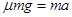 ⑨
⑨ ⑩
⑩得t=2s ⑾
评分标准:③式2分,其余各式1分

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 )求:
)求:
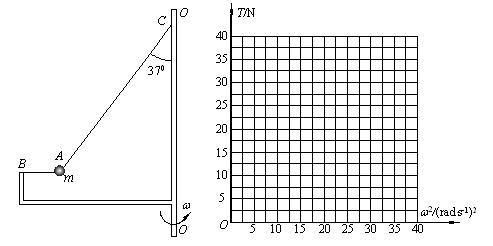
 时,细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°,求角速度
时,细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°,求角速度 时,细线AB刚好竖直,且张力为0,求此时角速度
时,细线AB刚好竖直,且张力为0,求此时角速度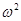 变化的关系图像
变化的关系图像
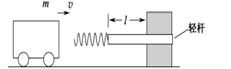
 时,装置可安全工作。 一质量为m 的小车若以速度
时,装置可安全工作。 一质量为m 的小车若以速度 撞击弹簧,可使轻杆向右移动了
撞击弹簧,可使轻杆向右移动了 。轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦。
。轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦。