题目内容
8.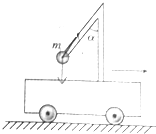 如图所示,小车上固定着一根弯成α角的曲杆,杆的另一端固定一个质量为m的球,当小车以加速度a水平向右运动时,求杆对球的弹力的大小和方向.
如图所示,小车上固定着一根弯成α角的曲杆,杆的另一端固定一个质量为m的球,当小车以加速度a水平向右运动时,求杆对球的弹力的大小和方向.
分析 先根据运动情况确定加速度大小和方向,然后受力分析,根据牛顿第二定律并结合正交分解法列式求解.
解答 解:小车以加速度a向右匀加速运动,小球受重力和弹力,合力为ma,水平向右,
根据牛顿第二定律,有:
水平方向:Fx=ma
竖直方向:Fy=mg
故合力:F=√F2x+F2y=m√a2+g2,
与水平方向的夹角的正切:
tanθ=FyFx=ga
则θ=arctanga
答:杆对球的弹力的大小m√a2+g2,和方向与水平方向夹角arctanga.
点评 本题是已知运动情况确定受力情况的问题,关键是先求解出加速度;注意杆的弹力与细线的弹力不同,杆的弹力可以与杆平行,也可以与杆不平行,可以是拉力,也可以是支持力.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
18. 嫦娥二号卫星已成功发射,这次发射后卫星直接进入近地点高度200公里、远地点高度约38万公里的地月转移轨道直接奔月.当卫星到达月球附近的特定位置时,卫星就必须“急刹车”,也就是近月制动,以确保卫星既能被月球准确捕获,又不会撞上月球,并由此进入近月点100公里、周期12小时的椭圆轨道a.再经过两次轨道调整,进入100公里的近月圆轨道b.轨道a和b相切于P点,如图所示.下列说法正确的是( )
嫦娥二号卫星已成功发射,这次发射后卫星直接进入近地点高度200公里、远地点高度约38万公里的地月转移轨道直接奔月.当卫星到达月球附近的特定位置时,卫星就必须“急刹车”,也就是近月制动,以确保卫星既能被月球准确捕获,又不会撞上月球,并由此进入近月点100公里、周期12小时的椭圆轨道a.再经过两次轨道调整,进入100公里的近月圆轨道b.轨道a和b相切于P点,如图所示.下列说法正确的是( )
 嫦娥二号卫星已成功发射,这次发射后卫星直接进入近地点高度200公里、远地点高度约38万公里的地月转移轨道直接奔月.当卫星到达月球附近的特定位置时,卫星就必须“急刹车”,也就是近月制动,以确保卫星既能被月球准确捕获,又不会撞上月球,并由此进入近月点100公里、周期12小时的椭圆轨道a.再经过两次轨道调整,进入100公里的近月圆轨道b.轨道a和b相切于P点,如图所示.下列说法正确的是( )
嫦娥二号卫星已成功发射,这次发射后卫星直接进入近地点高度200公里、远地点高度约38万公里的地月转移轨道直接奔月.当卫星到达月球附近的特定位置时,卫星就必须“急刹车”,也就是近月制动,以确保卫星既能被月球准确捕获,又不会撞上月球,并由此进入近月点100公里、周期12小时的椭圆轨道a.再经过两次轨道调整,进入100公里的近月圆轨道b.轨道a和b相切于P点,如图所示.下列说法正确的是( )| A. | 嫦娥二号卫星的发射速度大于11.2km/s | |
| B. | 嫦娥二号卫星的发射速度大于7.9km/s,小于11.2km/s | |
| C. | 嫦娥二号卫星在a、b轨道经过P点的速度va=vb | |
| D. | 嫦娥二号卫星在a、b轨道经过P点的加速度分别为aa、ab则aa=ab |
13. A、B、C三物体同时、同地、同向出发做直线运动,如图是它们位移-时间图象,由图可知它们在0到t0时间内( )
A、B、C三物体同时、同地、同向出发做直线运动,如图是它们位移-时间图象,由图可知它们在0到t0时间内( )
 A、B、C三物体同时、同地、同向出发做直线运动,如图是它们位移-时间图象,由图可知它们在0到t0时间内( )
A、B、C三物体同时、同地、同向出发做直线运动,如图是它们位移-时间图象,由图可知它们在0到t0时间内( )| A. | 平均速度vA=vB=vC | B. | 平均速率vA>vC>vB | ||
| C. | C一定做匀变速直线运动 | D. | A的速度一直比B、C大 |
14.关于物体的重力和重心,下列说法中正确的是( )
| A. | 重力的方向一定垂直于接触面 | |
| B. | 形状规则的物体,其重心一定在物体的几何中心 | |
| C. | 物体重心的位置跟物体的形状和质量分布有关 | |
| D. | 重心是重力的作用点,所以重心一定在物体上 |
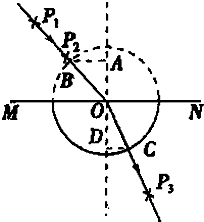 某同学用插针法测定一半圆形玻璃砖的折射率,实验后留下的痕迹如图所示,设AB的长度为l1,AO的长度为l2,CD的长度为l3,DO的长度为l4,为较方便地表示出玻璃砖的折射率,只需用刻度尺测量l1和l3(选填l1、l2、l3或l4),则玻璃砖的折射率可表示为
某同学用插针法测定一半圆形玻璃砖的折射率,实验后留下的痕迹如图所示,设AB的长度为l1,AO的长度为l2,CD的长度为l3,DO的长度为l4,为较方便地表示出玻璃砖的折射率,只需用刻度尺测量l1和l3(选填l1、l2、l3或l4),则玻璃砖的折射率可表示为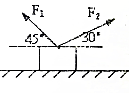 质量为6kg的物体放在水平面上,对物体施加两个拉力大小分别为F1=20
质量为6kg的物体放在水平面上,对物体施加两个拉力大小分别为F1=20