题目内容
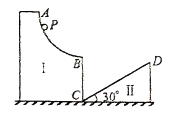
【题目】如图，I、II为极限运动中的两部分赛道，其中I的AB部分为竖直平面内半径为R的
光滑圆弧赛道，最低点B的切线水平; II上CD为倾角为30°的斜面，最低点C处于B点的正下方，B、C两点距离也等于R.质量为m的极限运动员(可视为质点)从AB上P点处由静止开始滑下，恰好垂直CD落到斜面上。求:
(1) 极限运动员落到CD上的位置与C的距离;
(2)极限运动员通过B点时对圆弧轨道的压力;
(3)P点与B点的高度差。
【答案】（1）
（2）
，竖直向下（3）
【解析】
（1）设极限运动员在B点的速度为v0，落在CD上的位置与C的距离为x，速度大小为v，在空中运动的时间为t，则xcos300=v0t
R-xsin300=
gt2
解得x=0.8R
（2）由（1）可得：
通过B点时轨道对极限运动员的支持力大小为FN
极限运动员对轨道的压力大小为FN′，则FN′=FN，
解得
，方向竖直向下；
（3） P点与B点的高度差为h,则mgh=mv02
解得h=R/5
练习册系列答案
相关题目
