题目内容
(9分)如图所示,矩形ABCD为长方体水池的横截面,宽度d=6m,高h= 水池里装有高度为h'=
水池里装有高度为h'=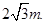 、折射率为n=
、折射率为n=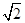 的某种液体,在水池底部水平放置宽度d=5cm的平面镜,水池左壁高b=
的某种液体,在水池底部水平放置宽度d=5cm的平面镜,水池左壁高b= 处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,考虑光在水池面上的反射,求在此横截面上标尺被照亮的长度和液面上能反射出光线部分的长度(结果保留2位有效数字)
处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,考虑光在水池面上的反射,求在此横截面上标尺被照亮的长度和液面上能反射出光线部分的长度(结果保留2位有效数字)
2.2m
解析试题分析: S发出的临界光线光路如图所示,
由几何关系有sinα= ①,根据折射定律有
①,根据折射定律有 ②
②
由①②解得:β=45°此横截面上标尺被照亮的长度x1=d-(b+h')tan30°-(h-h')tanβ,代入数据得:x1=2m,设此液体的临界角为θ,则sinθ= 所示θ=45°,则液面上能射出光线部分的长度
所示θ=45°,则液面上能射出光线部分的长度 ,代入数据得:
,代入数据得:
考点:本题考查几何知识在光学中的应用、折射定律。

练习册系列答案
相关题目
对于任何一种金属,要使它产生光电效应,必须满足的条件是( )
| A.入射光的强度要足够强 |
| B.入射光的照射时间要足够长 |
| C.入射光的频率要小于这种金属的极限频率 |
| D.入射光的频率要大于这种金属的极限频率 |
 的透明物质做成内、外径分别为
的透明物质做成内、外径分别为 、
、 的球壳,球壳的内表面涂有能完全吸收光的物质,如图所示,当一束平行光从左侧射向该球壳时,被吸收掉的光束在射进球壳左侧外表面前的横截面积有多大?
的球壳,球壳的内表面涂有能完全吸收光的物质,如图所示,当一束平行光从左侧射向该球壳时,被吸收掉的光束在射进球壳左侧外表面前的横截面积有多大?



 的玻璃柱体,其横截面是圆心角为90°,半径为R的扇形OAB。一束平行光平行于横截面,以45°入射角照射到0A上,0B不透光。若只考虑首次入射到圆弧AB上的光,则AB上有光透出部分的弧长为多长?
的玻璃柱体,其横截面是圆心角为90°,半径为R的扇形OAB。一束平行光平行于横截面,以45°入射角照射到0A上,0B不透光。若只考虑首次入射到圆弧AB上的光,则AB上有光透出部分的弧长为多长? 
 ,D点在AC边 上,AD间距为L。一条光线以60°的入射角从D点射入棱镜,光线垂直BC射出,求:
,D点在AC边 上,AD间距为L。一条光线以60°的入射角从D点射入棱镜,光线垂直BC射出,求:
