题目内容
【题目】在平面直角坐标系xoy中，x轴上方存在沿y轴负方向的匀强电场，电场强度为E，x轴下方存在垂直坐标平面向里的匀强磁场，磁感应强度为B。一个静止的带正电粒子位于y轴正半轴的A（0，h）点，某时刻由于内部作用，分裂成两个电荷量都为+q的粒子a和b，分别沿x轴正方向和负方向进入电场。已知粒子a的质量为m，粒子a进入第一象限的动量大小为p。设分裂过程不考虑外力的作用，在电场与磁场中的运动过程不计粒子重力和粒子间的相互作用。求：
（1）粒子a第一次通过x轴时离原点O的距离x；
（2）粒子a第二次通过x轴时与第一次通过x轴时两点间的距离L；
（3）若b粒子质量为a粒子质量的k倍，请利用（1）（2）中的结论推出xb与Lb的表达式。假设（1）（2）中的x=L，a粒子完成一个周期的运动时到达第一象限中的N点。现要使b粒子也能到达N点，试求k值应满足的条件。
【答案】（1）x＝p
（2）L＝
（3）
（其中n=1、2、3…，且k＞0）
【解析】试题分析：粒子a在电场中只受电场力，做类平抛运动，根据平抛运动公式求出粒子a第一次通过x轴时离原点O的距离x；粒子进入磁场后做匀速圆周运动，由洛伦兹力提供向心力，求出半径表达式，再根据几何关系求出粒子a第二次通过x轴时与第一次通过x轴时两点间的距离L; 两粒子在分裂过程中遵守动量守恒定律，粒子b进入电场的初动量大小也为p，方向沿x轴负方向，画出粒子的轨迹，根据几何关系求出k值应满足的条件。
（1）如图所示，粒子a在电场中只受电场力，做类平抛运动，轨迹如图所示
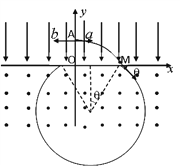
在水平方向：
在竖直方向：
粒子所受的电场力为：
粒子的动量为：
联立以上解得：
（2）粒子a进入磁场时，设速度为v，与x轴正方向成 角，则
在竖直方向有：
在竖直方向的分速度为：
粒子a在磁场中做匀速圆周运动，设轨迹半径为r，
由洛伦兹力提供向心力：
由几何知识得：
联立以上解得：
（3）两粒子在分裂过程中遵守动量守恒定律，粒子b进入电场的初动量大小也为p，方向沿x轴负方向。
由于b的质量为km，利用（1）（2）中的结论可得：
或
或
若a粒子运动过程中有x=L，则一个周期后达到N点离y轴距离就为3L。
要使粒子b也能到达N点，由于粒子b的运动是周期性运动，如图所示
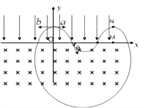
为粒子b一个周期恰好达到N点时的轨迹图。粒子b还可能经过
联立以上解得：
（其中n=1、2、3…,且k>0）
