题目内容
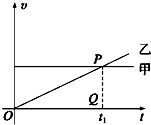 甲、乙两车在公路上沿同一方向做直线运动,它们的 v-t图象如图所示,两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,第二次相遇的时刻为t″,下列说法正确的是( )
甲、乙两车在公路上沿同一方向做直线运动,它们的 v-t图象如图所示,两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,第二次相遇的时刻为t″,下列说法正确的是( )| A、在t′时刻,乙车的速度大于甲车的速度 | ||||
B、如果第一次相遇的时刻t′=
| ||||
C、如果第一次相遇的时刻t′=
| ||||
D、如果第一次相遇的时刻t′=
|
分析:v-t图象中,与时间轴平行的直线表示做匀速直线运动,倾斜的直线表示匀变速直线运动,斜率表示加速度,倾斜角越大表示加速度越大,图象与坐标轴围成的面积表示位移.在时间轴上方的位移为正,下方的面积表示位移为负.相遇要求在同一时刻到达同一位置.
解答:解:A、由题意可知,相遇两次,所以刚开始甲在乙的前面,第一次相遇时,甲的速度大于乙的速度,后乙的速度大于甲的速度,这样就会有第二次相遇,故A错误;
B、从图象中甲、乙与坐标轴围成的面积即对应的位移看:当t′=
t1,由几何关系可知甲的面积比乙的面积多出
s,即相距d=
s时正好相遇,故B正确,C错误;
D、第二次相遇时,位移相同,则(t-
t1)?
=
?
(t-
t1)
解得:t=t″=
t1
即则第二次相遇时刻t″=
t1,故D正确
故选:BD
B、从图象中甲、乙与坐标轴围成的面积即对应的位移看:当t′=
| 1 |
| 3 |
| 5 |
| 9 |
| 5 |
| 9 |
D、第二次相遇时,位移相同,则(t-
| 1 |
| 3 |
| 2s |
| t1 |
| 1 |
| 2 |
| 2s |
| t1 |
| 1 |
| 3 |
解得:t=t″=
| 5 |
| 3 |
即则第二次相遇时刻t″=
| 5 |
| 3 |
故选:BD
点评:本题是速度--时间图象的应用,知道在速度--时间图象中图象与坐标轴围成的面积的含义,并能根据几何关系求出面积,能根据图象读取有用信息.

练习册系列答案
相关题目
 甲、乙两车在公路上沿同一方向做直线运动,在t=0时,乙车在甲车前50m处,它们的v-t图象如图所示,下列对汽车运动情况的描述正确的是( )
甲、乙两车在公路上沿同一方向做直线运动,在t=0时,乙车在甲车前50m处,它们的v-t图象如图所示,下列对汽车运动情况的描述正确的是( ) 甲、乙两车在公路上沿同一方向做直线运动,它们的 v-t图象如图所示.两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合可能的是( )
甲、乙两车在公路上沿同一方向做直线运动,它们的 v-t图象如图所示.两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合可能的是( ) 甲、乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示.在t=2s时,两车在途中相遇,则下列说法中正确的是( )
甲、乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示.在t=2s时,两车在途中相遇,则下列说法中正确的是( )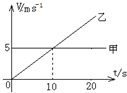 甲、乙两车在公路上沿同一方向做直线运动,它们的V-t图象如图所示.在t=0时刻,乙车在甲车前面,相距为25m,则下列说法正确的是( )
甲、乙两车在公路上沿同一方向做直线运动,它们的V-t图象如图所示.在t=0时刻,乙车在甲车前面,相距为25m,则下列说法正确的是( )