题目内容
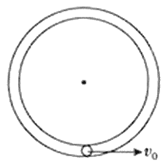
【题目】如图所示,固定在竖直平面内的圆管形轨道的外轨光滑,内轨粗糙。一小球从轨道的最低点以初速度v0向右运动,球的直径略小于圆管的直径,球运动的轨道半径为R,空气阻力不计,重力加速度大小为g,下列说法一定正确的是 ( )
A.若![]() ,小球不可能到达圆周最高点
,小球不可能到达圆周最高点
B.若![]() ,小球不可能到达圆周最高点
,小球不可能到达圆周最高点
C.若![]() ,小球运动过程中机械能守恒
,小球运动过程中机械能守恒
D.若![]() ,小球运动过程中机械能不守恒
,小球运动过程中机械能不守恒
【答案】BC
【解析】
AD. 小球如果不挤压内轨,则小球到达最高点速度最小时,小球的重力提供向心力,由牛顿第二定律,在最高点,有
![]()
由于小球不挤压内轨,则小球在整个运动过程中不受摩擦力作用,只有重力做功,机械能守恒,从最低点到最高点过程中,由机械能守恒定律,有
![]()
解得
![]()
若小球速度![]() ,小球也是有可能做完整的圆周运动的,可能到达圆周最高点,只是最终在圆心下方做往复运动,故A错误;若小球速度
,小球也是有可能做完整的圆周运动的,可能到达圆周最高点,只是最终在圆心下方做往复运动,故A错误;若小球速度![]() ,则小球一定不挤压内轨,小球运动过程中机械能守恒,故D错误;
,则小球一定不挤压内轨,小球运动过程中机械能守恒,故D错误;
B. 如果轨道内轨光滑,小球在运动过程中不受摩擦力,小球在运动过程中机械能守恒,如果小球运动到最高点时速度为0,由机械能守恒定律,有
![]()
解得
![]()
现在内轨粗糙,如果小球速度![]() ,小球在到达最高点前一定受到摩擦力作用,即小球在到达最高点前速度已为零,小球不可能到达圆周最高点,故B正确;
,小球在到达最高点前一定受到摩擦力作用,即小球在到达最高点前速度已为零,小球不可能到达圆周最高点,故B正确;
C.若小球上升到与圆心等高处时速度为零,此时小球只与外轨作用,不受摩擦力,只有重力做功,由机械能守恒定律,有
![]()
解得
![]()
若![]() ,小球只与外轨作用,不受摩擦力作用,小球运动过程中机械能守恒,故C正确。
,小球只与外轨作用,不受摩擦力作用,小球运动过程中机械能守恒,故C正确。
故选BC。

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案【题目】下表是卫星发射的几组数据,其中发射速度v0是燃料燃烧完毕时火箭具有的速度,之后火箭带着卫星依靠惯性继续上升,到达指定高度h后再星箭分离,分离后的卫星以环绕速度v绕地球做匀速圆周运动.根据发射过程和表格中的数据,下面哪些说法是正确的
卫星圆轨道离地面高度h(km) | 环绕速度v(km/s) | 发射速度v0(km/s) |
0 | 7.9 | 7.9 |
200 | 7.8 | 8.0 |
500 | 7.6 | 8.2 |
5000 | 5.5 | 9.5 |
A.不计空气阻力,在火箭依靠惯性上升的过程中机械能守恒
B.已知同步卫星的轨道离地高度约为36000km,其发射速度一定大于9.5km/s
C.卫星做匀速圆周运动离地越高,环绕周期越大
D.当发射速度达到11.2 km/s时,卫星能脱离太阳系的束缚