题目内容
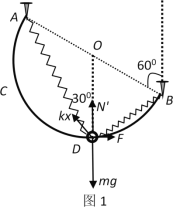
【题目】如图所示，半径为R的光滑半圆形导轨固定在竖直面内的AB两点，直径AB与竖直方向的夹角为60°，导轨上的C点在A点的正下方，D点是轨道的最低点，质量为m的圆环套在导轨上，圆环通过两个相同的轻弹簧分别与A、B两点连接，弹簧原长均为R，对圆环施加水平向右的力F=
可使其静止在D点。
(1)求弹簧的劲度系数k：
(2)由C点静止释放圆环，求圆环运动到D点的动能Ek；
(3)由C点静止释放圆坏，求圆环运动到D点时对轨道的作用力N。
【答案】（1）
；（2）
；（3）
，方向竖直向下
【解析】
(1)如图1所示，圆环在D点时，BD弹簧处于原长，AD弹簧的伸长量为x=
受力分析，正交分解
解得
(2)C点与D点的高度差 h=0.5R
圆环从C运动到D，弹簧弹性势能不变，根据机械能守恒
解得
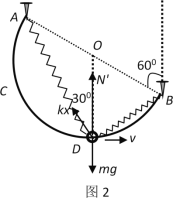
(3)如图2所示，圆环运动到D点时的速度
v=
受力分析，正交分解
解得
根据牛顿第三定律，圆环对轨道的作用力N为
方向竖直向下.
练习册系列答案
相关题目
