题目内容
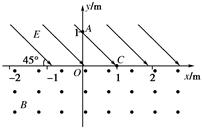
在如图所示的直角坐标系中,x轴的上方存在与x轴正方向成45°角斜向右下方的匀强电场,场强的大小为E=×104 V/m.x轴的下方有垂直于xOy面向外的匀强磁场,磁感应强度的大小为B=2×10-2 T.把一个比荷为 =2×108 C/kg的正电荷从坐标为(0,1)的A点处由静止释放.电荷所受的重力忽略不计.
=2×108 C/kg的正电荷从坐标为(0,1)的A点处由静止释放.电荷所受的重力忽略不计.

(1)求电荷从释放到第一次进入磁场时所用的时间;
(2)求电荷在磁场中做圆周运动的半径;(保留两位有效数字)
(3)当电荷第二次到达x轴时,电场立即反向,而场强大小不变,试确定电荷到达y轴时的位置坐标.
 =2×108 C/kg的正电荷从坐标为(0,1)的A点处由静止释放.电荷所受的重力忽略不计.
=2×108 C/kg的正电荷从坐标为(0,1)的A点处由静止释放.电荷所受的重力忽略不计.
(1)求电荷从释放到第一次进入磁场时所用的时间;
(2)求电荷在磁场中做圆周运动的半径;(保留两位有效数字)
(3)当电荷第二次到达x轴时,电场立即反向,而场强大小不变,试确定电荷到达y轴时的位置坐标.
(1)10-6 s (2)0.71 m (3)(0,8)
(1)如图,电荷从A点匀加速运动到x轴上C点的过程:
位移s=AC=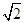 m
m
加速度a=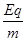 =2
=2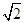 ×1012 m/s2
×1012 m/s2
时间t=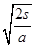 =10-6 s.
=10-6 s.
(2)电荷到达C点的速度为
v=at=2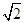 ×106 m/s
×106 m/s
速度方向与x轴正方向成45°角,在磁场中运动时
由qvB=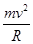
得R=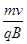 =
=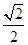 m
m
即电荷在磁场中的偏转半径为0.71 m.
(3)轨迹圆与x轴相交的弦长为Δx=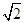 R=1 m,所以电荷从坐标原点O再次进入电场中,且速度方向与电场方向垂直,电荷在电场中做类平抛运动.
R=1 m,所以电荷从坐标原点O再次进入电场中,且速度方向与电场方向垂直,电荷在电场中做类平抛运动.

设电荷到达y轴的时间为t′,则:
tan 45°=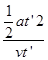
解得t′=2×10-6 s
则类平抛运动中垂直于电场方向的位移
L=vt′=4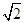 m
m
y= =8 m
=8 m
即电荷到达y轴时位置坐标为(0,8).
位移s=AC=
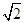 m
m
加速度a=
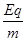 =2
=2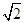 ×1012 m/s2
×1012 m/s2时间t=
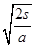 =10-6 s.
=10-6 s.(2)电荷到达C点的速度为
v=at=2
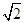 ×106 m/s
×106 m/s速度方向与x轴正方向成45°角,在磁场中运动时
由qvB=
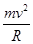
得R=
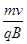 =
=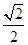 m
m即电荷在磁场中的偏转半径为0.71 m.
(3)轨迹圆与x轴相交的弦长为Δx=
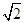 R=1 m,所以电荷从坐标原点O再次进入电场中,且速度方向与电场方向垂直,电荷在电场中做类平抛运动.
R=1 m,所以电荷从坐标原点O再次进入电场中,且速度方向与电场方向垂直,电荷在电场中做类平抛运动.
设电荷到达y轴的时间为t′,则:
tan 45°=
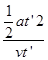
解得t′=2×10-6 s
则类平抛运动中垂直于电场方向的位移
L=vt′=4
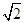 m
my=
 =8 m
=8 m即电荷到达y轴时位置坐标为(0,8).

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目


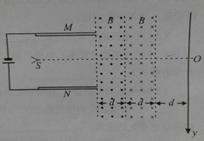
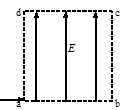
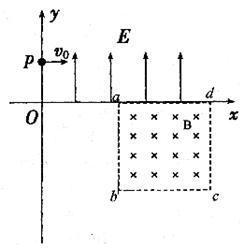
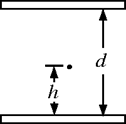
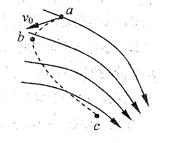
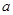 点以初速度
点以初速度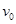 进入电场,沿虚线所示的轨迹运动到
进入电场,沿虚线所示的轨迹运动到 点,
点,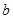 点为轨迹的最左端,如图所示,则粒子在从
点为轨迹的最左端,如图所示,则粒子在从