题目内容
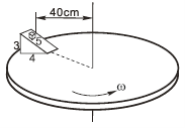
【题目】如图所示，一个边长满足3：4：5的斜面体沿半径方向固定在一水平转盘上，一木块静止在斜面上，斜面和木块之间的动摩擦系数μ=0.5。若木块能保持在离转盘中心的水平距离为40cm处相对转盘不动，g=10m/s2，则转盘转动角速度ω的可能值为（设最大静摩擦力等于滑动摩擦力）（ ）
A.2rad/sB.3rad/sC.4rad/sD.5rad/s
【答案】BCD
【解析】
根据题意可知斜面体的倾角满足
即重力沿斜面的分力大于滑动摩擦力，所以角速度为0时，木块不能够静止在斜面上。当转动的角速度较小时，木块所受的摩擦力沿斜面向上，则木块恰好向下滑动时
滑动摩擦力满足
解得
当转动角速度变大，木块恰好向上滑动时
滑动摩擦力满足
解得
所以圆盘转动的角速度满足
A错误，BCD正确。
故选BCD。
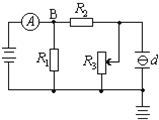
【题目】在“探究加速度与力、质量的关系”实验中，某同学组装了如图甲所示的装置．
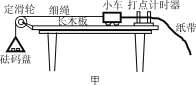
(1)关于平衡摩擦力的操作过程，下列说法正确的是________．
A. 应将长木板的左端适当垫高
B. 应将砝码盘通过细绳与小车相连
C. 应将纸带穿过打点计时器并与小车相连
D. 应使小车在长木板上保持静止
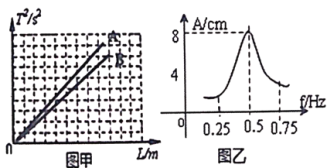
(2)平衡摩擦力后，保持砝码盘和砝码的总质量不变，改变小车的质量M，进行实验，算出加速度a，记录在如下的表格中．第3次实验的纸带如图乙所示，从比较清晰的点起，每五个点取一个计数点，分别标上0、1、2、3、4……，测得1与 2两点间距离x1＝30.0 mm，2与3两点间的距离x2＝32.5 mm，实验中所用交流电源的频率为50 Hz，由此算出加速度大小为________m/s2.
实验次数 | 1 | 2 | 3 | 4 | 5 |
小车质量M(kg) | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
加速度a(m/s2) | 0.77 | 0.38 | ________ | 0.19 | 0.15 |
(3)为了能直观地反映出小车的加速度a与质量M的关系，应作________(选填“a-M”或“
”)图象．
