题目内容
10.2016年1月20日,美国天文学家推侧,太阳系有第九大行星,该行星质量约为地球的10倍,半径约为地球的4倍,绕太阳一周需约2万年,冥王星比它亮约一万倍.已知地球的半径为R,地球表面的重力加速度为g,引力常量为G,地球和该行星绕太阳运动均视为匀速圆周运动.下列说法正确的是( )| A. | 太阳的质量约为$\frac{g{R}^{2}}{G}$ | |
| B. | 该行星的质量约为$\frac{10g{R}^{2}}{G}$ | |
| C. | 该行星表面的重力加速度约为$\frac{5}{8}$g | |
| D. | 该行星到太阳的距离约为地球的2万倍 |
分析 A、根据万有引力提供重力分析太阳的质量或地球的质量;
B、根据mg=$\frac{GMm}{{R}^{2}}$列式分析重力加速度的表达式进行分析;
C、根据mg=$\frac{GMm}{{R}^{2}}$列式分析重力加速度的表达式进行分析;
D、根据开普勒周期定律列式分析行星的公转半径.
解答 解:A、地球表面的物体的重力由万有引力提供,所以:mg=$\frac{G{M}_{地}m}{{R}^{2}}$,所以地球的质量:M地=$\frac{g{R}^{2}}{G}$.故A错误;
B、该行星质量是地球质量的10倍,M行星=10M地=$\frac{10g{R}^{2}}{G}$,故B正确;
C、根据mg=$\frac{GMm}{{R}^{2}}$,有g=$\frac{GM}{{R}^{2}}$;该行星质量是地球质量的10倍,半径约为地球的4倍,则$\frac{g}{g′}=\frac{{M}_{地}}{{M}_{行星}}•\frac{(4R)^{2}}{{R}^{2}}=\frac{16}{10}=\frac{8}{5}$,所以该行星表面的重力加速度约为$\frac{5}{8}$g.故C正确;
D、根据开普勒周期定律,有:$\frac{r_地^3}{T_地^2}=\frac{r_9^3}{T_9^2}$,解得:${r}_{9}=(\frac{{T}_{9}}{T})^{\frac{2}{3}}•r$=$\root{3}{(2×1{0}^{4})^{2}}•r$≈7.4×102r;故D错误;
故选:BC
点评 本题关键是明确行星和卫星的动力学原理,结合万有引力定律、开普勒定律和牛顿第二定律列式分析,不难.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.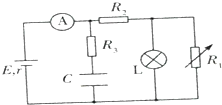 在如图所示的电路中,E为电源电动势,r为电源内阻,R1是半导体制成的NTC热敏电阻,其阻值随着温度的升高而减小,R2、R3为定值电阻,C为电容器,L为小灯泡,当所处环境温度下降时,则( )
在如图所示的电路中,E为电源电动势,r为电源内阻,R1是半导体制成的NTC热敏电阻,其阻值随着温度的升高而减小,R2、R3为定值电阻,C为电容器,L为小灯泡,当所处环境温度下降时,则( )
 在如图所示的电路中,E为电源电动势,r为电源内阻,R1是半导体制成的NTC热敏电阻,其阻值随着温度的升高而减小,R2、R3为定值电阻,C为电容器,L为小灯泡,当所处环境温度下降时,则( )
在如图所示的电路中,E为电源电动势,r为电源内阻,R1是半导体制成的NTC热敏电阻,其阻值随着温度的升高而减小,R2、R3为定值电阻,C为电容器,L为小灯泡,当所处环境温度下降时,则( )| A. | 电流表的示数增大 | B. | R2两端的电压增大 | ||
| C. | 小灯泡变暗 | D. | 电容器C所带的电荷量增大 |
5.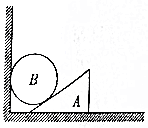 如图所示,粗糙水平地面上放有一斜面体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.把A向左移动少许后,它们仍处于静止状态,则( )
如图所示,粗糙水平地面上放有一斜面体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.把A向左移动少许后,它们仍处于静止状态,则( )
 如图所示,粗糙水平地面上放有一斜面体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.把A向左移动少许后,它们仍处于静止状态,则( )
如图所示,粗糙水平地面上放有一斜面体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.把A向左移动少许后,它们仍处于静止状态,则( )| A. | B对墙的压力增大 | B. | A对B的支持力减小 | ||
| C. | A对地面的压力增大 | D. | 地面对A的摩擦力不变 |
2.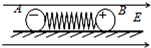 如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )
如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )
 如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )
如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )| A. | 因电场力分别对球A和球B做正功,故系统机械可能增加 | |
| B. | 因两个小球所受电场力等大反向,故系统机械能守恒 | |
| C. | 当弹簧长度达到最大值时,系统机械能最小 | |
| D. | 当小球所受电场力与弹簧的弹力相等时,系统动能最大 |
20.如图为物体做变速直线运动的v-t图象,令t=0时物体的位置为坐标原点,只研究前4s的运动,可知( )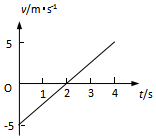
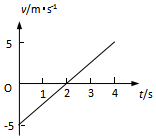
| A. | 物体始终沿正方向运动 | |
| B. | 物体先沿负方向运动,2s后开始沿正方向运动 | |
| C. | 在2s末物体回到坐标原点 | |
| D. | 在2s内物体的位移大小为5m |
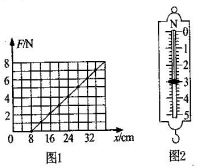 某同学在做“探究弹力和弹簧伸长的关系”实验时,通过处理数据得到了如图1所示的F-x图象,其中F为弹簧弹力,x为弹簧长度.
某同学在做“探究弹力和弹簧伸长的关系”实验时,通过处理数据得到了如图1所示的F-x图象,其中F为弹簧弹力,x为弹簧长度.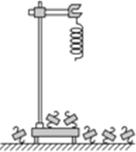 如图所示,用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系.
如图所示,用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系.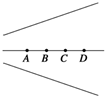 图为电场的电场线,现将一电荷量q=-3.0×10-9 C的负电荷从A点移到B点、从B点移到C点,从C点移到D点电场力做功分别为:WAB=3.0×10-8 J、WBC=1.5×10-8 J、WCD=9.0×10-9 J.若取C点电势为零,试求A、B、D三点电势.
图为电场的电场线,现将一电荷量q=-3.0×10-9 C的负电荷从A点移到B点、从B点移到C点,从C点移到D点电场力做功分别为:WAB=3.0×10-8 J、WBC=1.5×10-8 J、WCD=9.0×10-9 J.若取C点电势为零,试求A、B、D三点电势.