Question

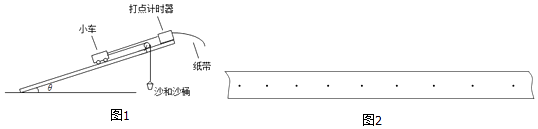
【题目】如图所示，一质量为mB=2 kg，长为L=6 m的薄木板B放在倾角为θ=30O的斜面面上，质量为mA=2 kg的物体A(可视为质点)在一平行于斜面的F=4N的力拉动下从木板左端以v0=5 m/s的速度沿斜面向下匀速运动。在物体带动下，木板以a=2 m/s2的加速度从静止开始做匀加速直线运动。已知B与斜面间的动摩擦因数μ1=，初始时刻B距斜面低端S=20m（如图所示），重力加速度g取10 m/s2，则

（1）经多长时间物体A滑离木板？

（2）AB间的动摩擦因数μ2是多少？

（3）若物体A滑离木板后立即取走物体A，木板滑到底端一共用时多少？

Answer 1

【答案】（1）2s（2） （3）6s

【解析】（1）设经t0时间物体A滑离木板，则对A：sA=v0t0

对木板B：

sA-sB=L

联立解得：t0=2s，（1分）t′=3s（舍去）

（2）物体A在沿斜面方向上受力平衡：μ2mgcosθ=mgsinθ+F

联立解得：

(3)A滑离B时B的速度为：v=at0=4m/s

位移：

A滑离木板后木板沿斜面上有摩擦力μ1mgcosθ=mgsinθ，故木板做匀速运动

从A滑离木板到木板滑到低端所经历的时间：

故一共用时：t=t0+t1=6s