题目内容
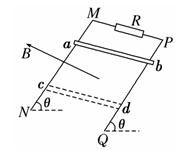
如图所示,MN、PQ为相距L=0.2 m的光滑平行导轨,导轨平面与水平面夹角为θ=30°,导轨处于磁感应强度为B=1 T、方向垂直于导轨平面向上的匀强磁场中,在两导轨的M、P两端接有一电阻为R=2 Ω的定值电阻,回路其余电阻不计.一质量为m=0.2 kg的导体棒垂直导轨放置且与导轨接触良好.今平行于导轨在导体棒的中点对导体棒施加一作用力F,使导体棒从ab位置由静止开始沿导轨向下匀加速滑到底端,滑动过程中导体棒始终垂直于导轨,加速度大小为a=4 m/s2,经时间t=1 s滑到cd位置,从ab到cd过程中电阻发热为Q=0.1 J,g取10 m/s2.求:
小题1:到达cd位置时,对导体棒施加的作用力;
小题2:导体棒从ab滑到cd过程中作用力F所做的功.

小题1:到达cd位置时,对导体棒施加的作用力;
小题2:导体棒从ab滑到cd过程中作用力F所做的功.
小题1:0.12 N,方向平行导轨向上
小题2:WF=-0.3 J.
(1)导体棒在cd处速度为:v=at=4 m/s (2分)
切割磁感线产生的电动势为:E=BLv=0.8 V (2分)
回路感应电流为:I==0.4 A (2分)
导体棒在cd处受安培力:F安=BIL=0.08 N (2分)
平行导轨向下为正方向:mgsinθ+F-F安=ma (2分)
解得:F=-0.12 N
对导体棒施加的作用力大小为0.12 N,方向平行导轨向上.(2分)
(2)ab到cd的距离:x=at2=2 m (2分)
根据功能关系:mgxsinθ+WF-Q=mv2-0 (2分)
解得:WF=-0.3 J. (2分)
切割磁感线产生的电动势为:E=BLv=0.8 V (2分)
回路感应电流为:I==0.4 A (2分)
导体棒在cd处受安培力:F安=BIL=0.08 N (2分)
平行导轨向下为正方向:mgsinθ+F-F安=ma (2分)
解得:F=-0.12 N
对导体棒施加的作用力大小为0.12 N,方向平行导轨向上.(2分)
(2)ab到cd的距离:x=at2=2 m (2分)
根据功能关系:mgxsinθ+WF-Q=mv2-0 (2分)
解得:WF=-0.3 J. (2分)

练习册系列答案
相关题目


 Wb
Wb



 角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直轨道平面的匀强磁场B,一根质量为m的金属杆MN从轨道上由静止滑下,经过足够长的时间后,流经金属棒的电流达到最大,金属杆做匀速运动,金属杆和轨道电阻均不计。则( )
角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直轨道平面的匀强磁场B,一根质量为m的金属杆MN从轨道上由静止滑下,经过足够长的时间后,流经金属棒的电流达到最大,金属杆做匀速运动,金属杆和轨道电阻均不计。则( )
