题目内容
如图所示，一个边长为L的正文形金属框，质量为m，电阻为R．用细线把它悬挂于一个有界的磁场边缘．金属框架的上半部处于磁场内，下半部处于磁场外．磁场随时间均匀变化满足B=kt规律．已知细线所能承受的最大拉力T0=2mg．求从t=0时起，经多长时间细线会被拉断．分析：根据法拉第电磁感应定律，与闭合电路欧姆定律，可求出感应电流大小，再由安培力表达式与受力平衡条件，即可求解．
解答：
解：要使细线拉断，磁场强度必须增大，此时有：
ε=
=
=
kL2
I=
=
（方向为逆时针）
对线框受力分析如图示；
F=BIL=
t
刚拉断时有：T0=mg+F
即为：2mg=mg+
t
∴t=
答：从t=0时起，经t=
时间细线会被拉断．
解：要使细线拉断，磁场强度必须增大，此时有：ε=
| △φ |
| △t |
| ||
| t |
| 1 |
| 2 |
I=
| ε |
| R |
| kL2 |
| 2R |
对线框受力分析如图示；
F=BIL=
| k2L3 |
| 2R |
刚拉断时有：T0=mg+F
即为：2mg=mg+
| k2L3 |
| 2R |
∴t=
| 2mgR |
| k2L3 |
答：从t=0时起，经t=
| 2mgR |
| k2L3 |
点评：考查法拉第电磁感应定律与闭合电路欧姆定律的应用，掌握安培力表达式，理解受力平衡方程．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
如图所示，一个边长为l、总电阻为R的单匝等边三角形金属线框，在外力的作用下以速度v匀速穿过宽度均为l的两个有界匀强磁场，磁场的磁感应强度大小均为B，方向相反．线框运动方向始终与底边平行且与磁场边界垂直．取顺时针方向的电流为正，从图示位置开始，线框中的感应电流i与线框沿运动方向的位移x之间的函数图象是（ ）
如图所示，一个边长为L的正方形线圈置于边界水平的匀强磁场上方L处，磁场宽为L，方向垂直纸面向里，由静止释放线圈且线圈平面始终与磁场方向垂直，如果从线圈的一边刚进入磁场开始计时，则下列关于通过线圈横截面的电荷量q、感应电流i、线圈运动加速度a、线圈具有的动能EK随时间变化的图象可能正确的是（ ）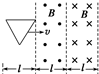
如图所示，一个边长为l、总电阻为R的单匝等边三角形金属线框，在外力的作用下以速度v匀速穿过宽度均为l的两个有界匀强磁场，磁场的磁感应强度大小均为B，方向相反．线框运动方向始终与底边平行且与磁场边界垂直．取顺时针方向的电流为正，从图示位置开始，线框中的感应电流i与线框沿运动方向的位移x之间的函数图象是（ ）
如图所示，一个边长为L的正方形金属框，质量为m、电阻为R，用细线把它悬挂于一个有界磁场边缘，金属框上半部分处于磁场内，磁场随时间均匀变化，满足B=kt关系．已知细线能承受最大拉力T=2mg，从t=0开始计时，经t=