题目内容
3.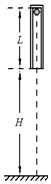 如图所示,一个质量为M长为L的圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=5m,球和管间的滑动摩擦力和最大静摩擦力大小均为5mg.管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求:
如图所示,一个质量为M长为L的圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=5m,球和管间的滑动摩擦力和最大静摩擦力大小均为5mg.管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求:(1)管第一次落地弹起时管和球的加速度;
(2)管第一次落地弹起后,若球没有从管中滑出,则球与管达到相同速度时,管的下端距地面的高度.
分析 (1)根据牛顿第二定律分别求出管反弹后,球和管的加速度.
(2)管自由下落,根据v02=2gH求出圆管底端落地前瞬间的速度.根据管上升的加速度,以及相对加速度分别求出管从碰地到它弹到最高点所需时间和管从碰地到与球相对静止所需的时间,比较两个时间知道球与管的运动情况,再根据运动学公式求出管上升的最大高度.
解答 解:(1)管第一次落地弹起时,管的加速度为:a1=$\frac{5mg+f}{M}$=$\frac{5mg+5mg}{5m}$=2g,方向向下
球的加速度为:a2=$\frac{f-mg}{m}$=$\frac{5mg-mg}{m}$=4g,方向向上.
(2)取竖直向下为正方向.球与管第一次碰地时速度 v0=$\sqrt{2gH}$,方向向下.
碰地后管的速度大小 v1=$\sqrt{2gH}$,方向向上;球的速度v2=$\sqrt{2gH}$,方向向下
若球刚好没有从管中滑出,设经过时间t1,球管速度v相同,
则有-v1+a1t1=v2-a2t1
解得 t1=$\frac{2{v}_{0}}{{a}_{1}+{a}_{2}}$=$\frac{2\sqrt{2gH}}{4g+2g}$=$\frac{\sqrt{2gH}}{3g}$
又管从碰地到它弹到最高点所需时间t2,则:t2=$\frac{{v}_{0}}{{a}_{1}}$=$\frac{\sqrt{2gH}}{2g}$
因为t1<t2,说明管在达到最高点前,球与管相对静止,故管从弹起经t1这段时间上升的高度为所求.得:
h1=v1t1-$\frac{1}{2}$a1t12=$\sqrt{2gH}$•$\frac{\sqrt{2gH}}{3g}$-$\frac{1}{2}•2g•(\frac{\sqrt{2gH}}{3g})^{2}$=$\frac{4}{9}$H
答:(1)管第一次落地弹起时管和球的加速度分别为2g方向竖直向下和4g方向竖直向上;
(2)管第一次落地弹起后,若球没有从管中滑出,则球与管达到相同速度时,管的下端距地面的高度为$\frac{4}{9}$H.
点评 本题的难点在于管和球的运动情况难于判断,关键通过计算理清球和管的运动规律,分析管和球之间的关系,如位移关系、速度关系,结合牛顿第二定律和运动学公式进行求解.

 如图质量为m的小球用水平弹簧系住,并用倾角为37°的光滑木板AB托住,小球恰好处于静止状态.已知sin37°=0.6,cos37°=0.8,重力加速度为g.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )
如图质量为m的小球用水平弹簧系住,并用倾角为37°的光滑木板AB托住,小球恰好处于静止状态.已知sin37°=0.6,cos37°=0.8,重力加速度为g.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )| A. | 大小为0 | B. | 大小为0.75g | C. | 大小为g | D. | 大小为1.25g |
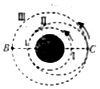 2016年10月17日,“神舟十一号”载人飞船发射升空,运送两名宇航员前往在2016年9月15日发射的“天宫二号”空间实验室,宇航员计划在“天宫二号”驻留30天进行科学实验.“神舟十一号”与“天宫二号”的对接变轨过程如图所示,AC是椭圆轨道Ⅱ的长轴.“神舟十一号”从圆轨道I先变轨到椭圆轨道Ⅱ,再变轨到圆轨道Ⅲ,与在圆轨道Ⅲ运行的“天宫二号”实施对接.下列描述正确的是( )
2016年10月17日,“神舟十一号”载人飞船发射升空,运送两名宇航员前往在2016年9月15日发射的“天宫二号”空间实验室,宇航员计划在“天宫二号”驻留30天进行科学实验.“神舟十一号”与“天宫二号”的对接变轨过程如图所示,AC是椭圆轨道Ⅱ的长轴.“神舟十一号”从圆轨道I先变轨到椭圆轨道Ⅱ,再变轨到圆轨道Ⅲ,与在圆轨道Ⅲ运行的“天宫二号”实施对接.下列描述正确的是( )| A. | “神舟十一号”在变轨过程中机械能不变 | |
| B. | 可让“神舟十一号”先进入圆轨道Ⅲ,然后加速追赶“天宫二号”实现对接 | |
| C. | “神舟十一号”从A到C的平均速率比“天宫二号”从B到C的平均速率大 | |
| D. | “神舟十一号”在椭圆轨道上运动的周期与“天宫二号”运行周期相等 |
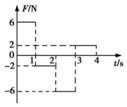 质量为m=1kg的物体静止于水平面上,现对物体施加一个水平外力F,外力F随时间t的变化关系如图所示,已知物体与水平面间的动摩擦因数μ=0.2,g=10m/s2,则下列对物体在0~4s内的情况判断正确的是( )
质量为m=1kg的物体静止于水平面上,现对物体施加一个水平外力F,外力F随时间t的变化关系如图所示,已知物体与水平面间的动摩擦因数μ=0.2,g=10m/s2,则下列对物体在0~4s内的情况判断正确的是( )| A. | 2s末物体离出发点最远 | |
| B. | 4s末物体离出发点最远 | |
| C. | 前2s内和后2s内物体所受摩擦力相同 | |
| D. | 4s内物体的平均速率为2m/s |
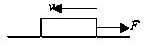 如图所示,重力G=20N的物体,在动摩擦因数为0.1的水平面上向左运动,同时受到大小为10N的,方向向右的水平力F的作用,则物体所受摩擦力大小和方向是( )
如图所示,重力G=20N的物体,在动摩擦因数为0.1的水平面上向左运动,同时受到大小为10N的,方向向右的水平力F的作用,则物体所受摩擦力大小和方向是( )| A. | 10N,水平向左 | B. | 2N,水平向左 | C. | 2N,水平向右 | D. | 12N,水平向 |
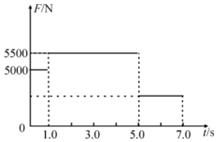 建筑工地上常用升降机将建材从地面提升到需要的高度,某次提升建材时,研究人员在升降机底板安装了压力传感器,可以显示建材对升降机底板压力的大小.已知建材放上升降机后,升降机先静止了t0=1s,然后启动,7s末刚好停止运动,在这7s内压力传感器的示数如图所示.当地重力加速度g取10m/s2.求:
建筑工地上常用升降机将建材从地面提升到需要的高度,某次提升建材时,研究人员在升降机底板安装了压力传感器,可以显示建材对升降机底板压力的大小.已知建材放上升降机后,升降机先静止了t0=1s,然后启动,7s末刚好停止运动,在这7s内压力传感器的示数如图所示.当地重力加速度g取10m/s2.求: