题目内容
11.有人设计了一种可测速的跑步机.测速原理如图所示,该机底面固定有间距为L、长度为d的平行金属电极.电极间充满磁感应强度为B、方向垂直纸面向里的匀强磁场,理想伏特表和电阻R并联后接在电极的两端.绝缘橡胶带上固定有间距为d的平行细金属条,橡胶带在电动机带动下运动时,金属条将随着橡胶带进入磁场区域,金属条跟电极接触良好,金属条的电阻均为r,其他部分的电阻均可忽略不计.
(1)写出橡胶带运动速度v跟伏特表示数U之间的表达式;
(2)橡胶带以速度v1匀速运动时,每根金属条穿过磁场区域克服安培力做的功;
(3)关闭电动机,运动员在跑步机上跑步时对橡胶带的静摩擦力也可以带动橡胶带运动,这种跑步机被称为机械式跑步机.假定橡胶带在此种情况下运动时受到的机械阻力跟速度的平方成正比,即f=kv2,k为比例常数,并且运动员消耗的体能全部用来维持橡胶带匀速运动.求橡胶带以速度v2匀速运动时运动员消耗的功率.
分析 (1)磁场中始终有一根金属条切割磁感线,产生感应电动势,相当于电源,电压表测量路端电压.由感应电动势公式E=BLv和欧姆定律等等知识求解.
(2)根据感应电动势公式E=BLv、欧姆定律和安培力公式F=BIL,求出安培力的大小,即可由功的公式求解克服安培力做的功.
(3)橡胶带匀速运动,运动员对橡胶带的摩擦力大小:F=f+F2,据题f=kv22,安培力F2=BI2L,运动员消耗的最小功率:P=Fv2,结合求解橡胶带以速度v2匀速运动时运动员消耗的功率P.
解答 解:(1)金属条做切割磁感线运动产生的电动势大小为:E=BLv
回路中的电流大小为:I=$\frac{E}{R+r}$
伏特表的示数为:U=IR
解得:v=$\frac{R+r}{BLR}U$
(2)金属条中的电流为:I1=$\frac{BL{v}_{1}}{R+r}$
金属条受的安培力大小为:F1=BI1L
金属条克服安培力做功为:W=F1d=$\frac{{B}^{2}{L}^{2}d{v}_{1}}{R+r}$
(3)运动员对橡胶带的摩擦力大小为:F=f+F2
据题有:f=kv2
又 F2=BI2L=$\frac{{B}^{2}{L}^{2}{v}_{2}}{R+r}$
运动员消耗的最小功率为:P=Fv2=( f+F2)v2
联立得:P=${v}_{2}^{2}$(kv2+$\frac{{B}^{2}{L}^{2}}{R+r}$)
答:(1)橡胶带运动速度v跟伏特表示数U之间的表达式为v=$\frac{R+r}{BLR}U$.
(2)每根金属条穿过磁场区域克服安培力做的功是$\frac{{B}^{2}{L}^{2}d{v}_{1}}{R+r}$.
(3)橡胶带以速度v2匀速运动时运动员消耗的功率为${v}_{2}^{2}$(kv2+$\frac{{B}^{2}{L}^{2}}{R+r}$).
点评 本题是理论联系实际问题,关键是建立物理模型,综合运用电磁感应知识、电路知识、力学知识解题,要有分析和解决实际问题的能力.

 阅读快车系列答案
阅读快车系列答案 如图所示的交流电路中.理想变压器输入电压为U1,输人功率为P1,输出功率为P2,各电表均为理想交流电表,则当滑动变阻器R的滑动触头( )
如图所示的交流电路中.理想变压器输入电压为U1,输人功率为P1,输出功率为P2,各电表均为理想交流电表,则当滑动变阻器R的滑动触头( )| A. | 向下移动时,灯L变亮 | |
| B. | 向上移动时,变压器输入电流减小 | |
| C. | 向下移动时,各个电表示数均变大 | |
| D. | 向上移动时,P1增大,且始终有P1=P2 |
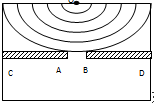 如图所示是观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个孔,O是波源,图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间距离表示一个波长,则波经过孔之后的传播情况,下列描述正确的是 ( )
如图所示是观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个孔,O是波源,图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间距离表示一个波长,则波经过孔之后的传播情况,下列描述正确的是 ( )| A. | 此时能明显观察到波的衍射现象 | |
| B. | 挡板前后波纹间距离相等 | |
| C. | 如果将孔AB扩大,有可能观察不到明显的衍射现象 | |
| D. | 如果孔的大小不变,使波源频率增大,能更明显地观察到衍射现象 | |
| E. | 挡板前后波纹间距离不等 |
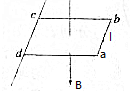 如图所示,匀强磁场的磁感应强度为B,方向竖直向下,在磁场中有边长为1的正方形导线框,ab边质量为m,其余边质量不计,cd边有周定的水平轴,导线框可以绕其转动.现将导线框拉至水平位置由静止释放,不计摩擦和空气阻力,金属框经过时间t运动到竖直位置,此时ab边的速度为v,求:
如图所示,匀强磁场的磁感应强度为B,方向竖直向下,在磁场中有边长为1的正方形导线框,ab边质量为m,其余边质量不计,cd边有周定的水平轴,导线框可以绕其转动.现将导线框拉至水平位置由静止释放,不计摩擦和空气阻力,金属框经过时间t运动到竖直位置,此时ab边的速度为v,求:
 如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg.当AC和BC均拉直时∠ABC=90°,∠BAC=37°,BC=0.3m.竖直轴AB匀速转动,C球在水平面内做匀速圆周运动.求:(g取10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg.当AC和BC均拉直时∠ABC=90°,∠BAC=37°,BC=0.3m.竖直轴AB匀速转动,C球在水平面内做匀速圆周运动.求:(g取10m/s2,sin37°=0.6,cos37°=0.8)