题目内容
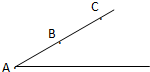 一物体以一定的初速度从一光滑斜面底端A点上滑,最高可滑至C点,B是AC的中点,如图所示,已知物块从A至B需时间为t0,问它从B经C再回到B,需要的时间是多少?
一物体以一定的初速度从一光滑斜面底端A点上滑,最高可滑至C点,B是AC的中点,如图所示,已知物块从A至B需时间为t0,问它从B经C再回到B,需要的时间是多少?分析:匀减速直线运动问题可以用其逆过程,相当于初速度为零的匀加速直线运动,结合运动学关系式可以解出所需的时间.
解答:解:设物体从A到C所用时间为t,从B到C所用时间为t1则
t1=t-t0 ①
设AC长度为L,物体运动加速度为a,
由匀变速直线运动的位移速度关系式,根据A到C的逆过程,
得:L=
at2 ②
从B到C由根据逆过程得:
L=
a
③
①②③联立可得 t1=(
+1)t0
由对称性,从B到C再回B所用时间t2=2t1=2(
+1)t0
答:它从B经C再回到B,需要的时间是2(
+1)t0
t1=t-t0 ①
设AC长度为L,物体运动加速度为a,
由匀变速直线运动的位移速度关系式,根据A到C的逆过程,
得:L=
| 1 |
| 2 |
从B到C由根据逆过程得:
| 1 |
| 2 |
| 1 |
| 2 |
| t | 2 1 |
①②③联立可得 t1=(
| 2 |
由对称性,从B到C再回B所用时间t2=2t1=2(
| 2 |
答:它从B经C再回到B,需要的时间是2(
| 2 |
点评:注意要灵活应用匀减速直线运动的逆过程,会使题目解题难度大大减小,有利于解题.

练习册系列答案
相关题目
 (2010?东城区三模)如图所示,一物体以一定的初速度沿水平地面从A点滑到B点,摩擦力做功为W1;若该物体从A′点沿两斜面滑到B′点(物体始终没有离开斜面),摩擦力做的总功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
(2010?东城区三模)如图所示,一物体以一定的初速度沿水平地面从A点滑到B点,摩擦力做功为W1;若该物体从A′点沿两斜面滑到B′点(物体始终没有离开斜面),摩擦力做的总功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
 如图,一物体以一定的初速度沿水平面由A点滑到B点,摩擦力做功为W1;若该物体从A′点沿斜面滑到B′点,摩擦力做功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
如图,一物体以一定的初速度沿水平面由A点滑到B点,摩擦力做功为W1;若该物体从A′点沿斜面滑到B′点,摩擦力做功为W2,已知物体与各接触面的动摩擦因数均相同,则( )