��Ŀ����
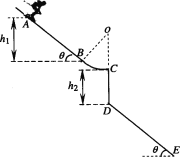
����Ŀ����ͼ��ʾ��BCΪ�뾶R=2.5m�� ![]() Բ����ABΪ�⻬ˮƽ������������B���������ӣ�AB����ϵĻ���Pͨ�����쳤��������������ֱ�⻬ϸ�˵Ļ���Q���ӣ���ʼʱ��P��A����Q����Aͬһˮƽ���ϵ�E���������Ӹպ���ֱ����ˮƽ���̶���С������D����DE=3m���ƻ��������Ӽ��Ħ���Ϳ����������ְ�Q�Ӿ�ֹ�ͷţ�������h=3mʱ��Pǡ�õ���Բ�������B���Ҷ�B��ѹ����ȡg=10m/s2 �� ����
Բ����ABΪ�⻬ˮƽ������������B���������ӣ�AB����ϵĻ���Pͨ�����쳤��������������ֱ�⻬ϸ�˵Ļ���Q���ӣ���ʼʱ��P��A����Q����Aͬһˮƽ���ϵ�E���������Ӹպ���ֱ����ˮƽ���̶���С������D����DE=3m���ƻ��������Ӽ��Ħ���Ϳ����������ְ�Q�Ӿ�ֹ�ͷţ�������h=3mʱ��Pǡ�õ���Բ�������B���Ҷ�B��ѹ����ȡg=10m/s2 �� ����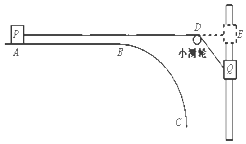
��1����P����B��ʱ��P���ٶȴ�С��
��2����P����B��ʱ��Q���ٶȴ�С��
��3������P��Q������֮�ȣ��� ![]() =��
=��
���𰸡�
��1���⣺Pǡ�õ���Բ�������B�����Ҷ�B��ѹ�����������ṩ����������ã�
mPg=mP ![]()
��ã�vP= ![]() =
= ![]() =5m/s
=5m/s
����P����B��ʱ��P���ٶȴ�СΪ5m/s
��2���⣺P����B��ʱ��DQ���������ϸ�˼�ļн�Ϊ45�㣮
����P��Q�����ӷ���ķ��ٶȴ�С��ȣ��У�
vQcos45��=vP��
��ã�vQ=5 ![]() m/s
m/s
����P����B��ʱ��Q���ٶȴ�СΪ5 ![]() m/s
m/s
��3���⣺P��Q���˶�������ֻ��������������ϵͳ�����ݶ��ܶ����ã�
![]() mPvP2+
mPvP2+ ![]() mQvQ2=mQgh
mQvQ2=mQgh
����������12.5mP+25mQ=30mQ
��ã� ![]() =
= ![]()
�𣺻���P��Q������֮��Ϊ2��5
����������1��Pǡ�õ���Բ�������B���Ҷ�B��ѹ�����������ṩ��������������������ʽ���P����B��ʱ���ٶȣ���2��P����B��ʱ�����ӵ��ٶȵ���P���ٶȣ�����P��Q�����ӷ���ķ��ٶȴ�С��ȣ��������Q���ٶȣ���3��P��Q���ɵ�ϵͳ���˶�������ֻ���������������ݶ��ܶ�����ʽ�����������֮�ȣ�
�����㾫�������ö��ܶ������ۺ�Ӧ�ö���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�