题目内容
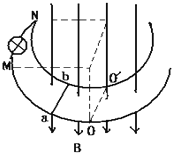
【题目】如图所示，竖直平面内的四分之一圆弧轨道下端与水平桌面相切，小滑块A和B分别静止在圆弧轨道的最高点和最低点。现将A无初速释放，A与B碰撞后结合为一个整体，并沿桌面滑动。已知圆弧轨道光滑，半径R=0.2 m；A和B的质量相等；A和B整体与桌面之间的动摩擦因数μ=0.2。取重力加速度g=10 m/s2。求：
（1）碰撞前瞬间A的速率v；
（2）碰撞后瞬间A和B整体的速率v′；
（3）A和B整体在桌面上滑动的距离l。
【答案】（1）碰撞前瞬间A的速率为2m/s；
（2）碰撞后瞬间A和B整体的速率为1m/s；
（3）A和B整体在桌面上滑动的距离为0.25m．
【解析】试题分析：（1）滑块从圆弧最高点滑到最低点的过程中，根据机械能守恒定律，有：
，得：
．
（2）滑块A与B碰撞，轨道向右为正方向，根据动量守恒定律，有：
，得：
．
（3）滑块A与B粘在一起滑行，根据动能定理，有：
又因为：
，代入数据联立解得：
．
冲刺100分1号卷系列答案【题目】某同学在“用打点计时器测速度”的实验中，用打点计时器记录了被小车拖动的纸带的运动情况，在纸带上确定出A、B、C、D、E、F、G共7个计数点．其相邻点间的距离如图所示，每两个相邻的测量点之间的时间间隔为0.10s．
（1）试根据纸带上各个计数点间的距离，每个0.10s测一次速度，计算出打下B、C、D、E、F五个点时小车的瞬时速度，并将各个速度值填入下表（结果要求保留3位有效数字）
vB | vC | vD | vE | vF | |
数值（m/s） | ____ | ____ | ____ | ____ | ____ |
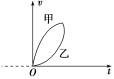
（2）将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中，并在图中画出小车的瞬时速度随时间变化的关系图线．
（______________）
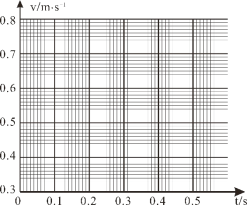
（3）由v﹣t图象可知打下A点时小车的瞬时速度vA=________，打下G点时小车的瞬时速度vB=________．
【题目】某同学在探究小车速度随时间变化的规律时，对打出的一条纸带进行研究，从O点开始每5个打点作为一个计数点（中间4个打点未画出，电源频率为50赫兹），计数点分别为A、B、C、D、E，该同学已求出各计数点对应的速度，其数值见下表。（结果保留两位有效数字）
（1）根据以上数据在所给的坐标纸中作出小车的v-t图线______（计数点O点为计时起点，适当标出横、纵坐标刻度）。
计数点 | A | B | C | D | E |
速度/（m·s-1） | 0.70 | 0.91 | 1.10 | 1.30 | 1.49 |
（2）计数点O对应的速度为______ m/s，加速度为______ m/s2。（保留3位有效数字）
