题目内容
【题目】为了“探究做功与速度变化的关系”,现提供如图所示实验装置。
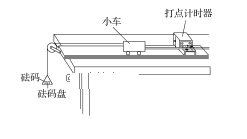
以下为该实验中的部分内容:
(1)在实验中,得到一条如图所示的纸带,已知相邻计数点间还有四个点未画出,打点计时器的频率为50Hz,且间距x1、x2、x3、x4、x5、x6已量出分别为3.09cm、3.43cm、3.77cm、4.10cm、4.44cm、4.77cm,则小车的加速度大小为_____m/s2,小车在打点计时器打下F点时的速度大小为_____m/s(结果保留两位有效数字)。

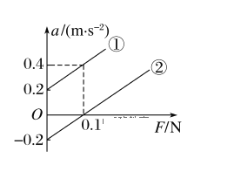
(2)由于该实验中小车的质量和阻力未知,由另一组同学设计了以下实验来测算小车的质量和小车在水平长木板上运动时所受的阻力,实验中保持小车质量一定,且远大于砝码盘及盘中砝码的总质量,他们在轨道水平及倾斜两种情况下分别做了实验,得到了两条a-F图线。如图所示,图线_____是在轨道倾斜情况下得到的(填“①”或“②”)。由图像可求得小车的质量m=_____kg,小车在水平运动时所受到的阻力f=________N。
【答案】(1)0.34, 0.46 (2)① 0.5 0.1
【解析】
(1)由匀变速运动的规律得:
s4-s1=3aT2
s5-s2=3aT2
s6-s3=3aT2
联立得:(s4+s5+s6)-(s1+s2+s3)=9aT2
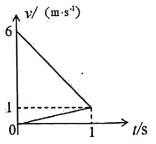
解得:![]()
小车在打点计时器打下F点时的速度大小为![]()
(2)由图象可知,当F=0时,a≠0.也就是说当绳子上没有拉力时小车就有加速度,该同学实验操作中平衡摩擦力过大,即倾角过大,平衡摩擦力时木板的右端垫得过高。所以图线①是在轨道右侧抬高成为斜面情况下得到的。
根据F=ma得a-F图象的斜率k=![]() ,由a-F图象得图象斜率k=2,所以m=0.5kg。图像②是在水平轨道运动得到的图像,由图像可知当F=0.1N时小车才有加速度,可知小车在水平轨道上所受的阻力f=0.1N.
,由a-F图象得图象斜率k=2,所以m=0.5kg。图像②是在水平轨道运动得到的图像,由图像可知当F=0.1N时小车才有加速度,可知小车在水平轨道上所受的阻力f=0.1N.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案