题目内容
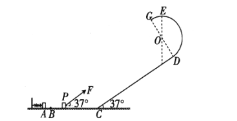
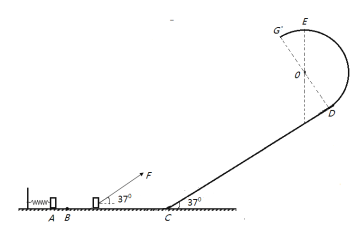
【题目】如图所示轻弹簧一端固定在水平面上的竖直挡板上,处于原长时另一端位于水平面上B点处,B点左侧光滑,右侧粗糙。水平面的右侧C点处有一足够长的斜面与水平面平滑连接,斜面倾角为37°,斜面上有一半径为R=1m的光滑半圆轨道与斜面切于D点,半圆轨道的最高点为E,G为半圆轨道的另一端点,
=2.5m,A、B、C、D、E、G均在同一竖直面内。使质量为m=0.5kg的小物块P挤压弹簧右端至A点,然后由静止释放P,P到达B点时立即受到斜向右上方,与水平方向的夹角为37°,大小为F=5N的恒力,一直保持F对物块P的作用,结果P通过半圆轨道的最高点E时的速度为
。已知P与水平面斜面间的动摩擦因数均为μ=0.5,g取
.sin37°=0.6,
(1)P运动到E点时对轨道的压力大小;
(2)弹簧的最大弹性势能;
(3)若其它条件不变,增大B、C间的距离使P过G点后恰好能垂直落在斜面上,求P在斜面上的落点距D点的距离。
【答案】（1）
(2) 
(3) 
【解析】
(1) P在半圆轨道的最高点E，设轨道对P的压力为，由牛顿运动定律得：
解得：
由牛顿第三定律得，P运动到E点时对轨道的压力FN =3N
(2)P从D点到E点，由动能定理得：
解得：
m/s
P从C点到D点，由牛顿运动定律得：
解得
，说明P从C点到D点匀速运动，故
由能的转化和守恒得：
解得：
J
（3）P在G点脱离圆轨道，做曲线运动，把该运动分解为平行于斜面的匀减速直线运动和垂直于斜面的初速度为零的匀加速直线运动，有：
解得：
m/s2
解得：
m/s2
P垂直落在斜面上，运动时间满足：
平行于斜面方向上：
联立解得：
m/s
平行于斜面方向上：
m
P在斜面上的落地距D的距离
m。
练习册系列答案
相关题目
