题目内容
如图所示,倾角为θ=30°的光滑斜面体P的底端带有固定挡板C,P和C的总质量为M.劲度系数为k的轻质弹簧两端连接质量均为m的小物块A和B,B紧靠着挡板.一轻质细绳通过定滑轮,一端系在物块A上,另一端系一细绳套(细绳与斜面平行,不计绳与滑轮间的摩擦,细绳套离地面足够高).开始时,斜面体P、物块A、B静止在光滑水平面上,细绳处于伸直状态.
(1)现开始用一水平力F作用于P,且能使物块B刚要离开挡板C。求此时力F的大小及从开始到此时物块A相对斜面体P的位移的大小d;
(2)若将斜面体P固定在水平面上,当在细绳套上轻轻挂上一个物体D后由静止释放,物体B恰能离开C,求物体D的质量mD;
(3)若将斜面体P固定在水平面上,当在细绳套上轻轻挂一个质量也为m的物体Q后由静止释放,求物体A能达到的最大速度。

(1)开始时,弹簧压缩了x1,则对A有:
kx1=mgsinθ
当B刚要离开C时,由于A、B的质量相等,合力也相同,所以弹簧无形变。
从开始到此时物体A相对斜面体P的位移大小d= x1=![]() =
=![]() .
.
对P、A、B用整体法分析,根据牛顿第二定律得:F=(M+2m)a,
对A、B用整体法分析有:2mgtanθ=2ma
解得:F=(M+2m)g tanθ=![]() .
.
(2)物体B恰好离开挡板C时,弹簧伸长了x2,则
Kx2=mgsin300
∴x2=x1,即弹性势能不变
由机械能守恒得:
mDg(x1+x2)=mAg· sin300(x1+x2)
解得 mD=![]() m
m
(3)当物体A受到的加速度为0时,速度最大,此时Q的加速度也为0
挂物体Q前,弹簧被压缩了x1,
当物体A受到的合力为0时,设弹簧被拉伸了x3,则
Kx3+mgsin300=mg
由上可知x1=x3,即弹性势能不变,且此时B的速度仍为0
设物体A的最大速度为vm,由机械能守恒定律得
mQg(x1+x3)-mAg sin300(x1+x3)=![]() (mQ+mA)vm2
(mQ+mA)vm2
解得:vm=![]()

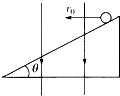 如图所示,倾角为θ的斜面处于竖直向下的匀强电场中,在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球,小球在电场中受到的电场力与小球所受的重力相等,地球表面重力加速度为g,设斜面足够长.问:
如图所示,倾角为θ的斜面处于竖直向下的匀强电场中,在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球,小球在电场中受到的电场力与小球所受的重力相等,地球表面重力加速度为g,设斜面足够长.问: 如图所示,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8. 如图所示,倾角为θ的斜面上有一质量为m的物体,在水平推力F的作用下移动了距离s,如果物体与斜面间的动摩擦因数为μ,则推力所做的功为( )
如图所示,倾角为θ的斜面上有一质量为m的物体,在水平推力F的作用下移动了距离s,如果物体与斜面间的动摩擦因数为μ,则推力所做的功为( ) (2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )
(2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )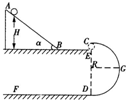 如图所示,倾角为α的光滑斜面与半径为R=0.4m的半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4m,直径CD沿竖直方向,C、E可看作重合.现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的
如图所示,倾角为α的光滑斜面与半径为R=0.4m的半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4m,直径CD沿竖直方向,C、E可看作重合.现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的