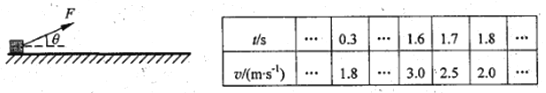题目内容
【题目】如图所示，左侧地面上固定着圆心为O、半径为R的光滑圆弧，圆弧上端B点与O点连线与竖直方向夹角为θ=53°，下端与静止在光滑水平面上的平板车CD上端相切，平板车上表面粗糙，且水平部分长度为l=5m，平板车右端是一
光滑圆弧轨道，平板车的质量为m=2.3kg，平板车左端C点正上方放一质量为m2=2.3kg物块Q(可视为质点)，且Q左侧粘贴有少量火药(质量不计)。一质量为m1=1kg的小滑块P从距离平板车上方高度为h=8m处的A点以v0=6m/s的初速度水平抛出，恰好从B点沿切线方向进入轨道，当滑块运动到C处与物块Q发生弹性正碰的同时火药爆炸，使P、Q分别向两侧运动。当滑块P沿轨道返回经过F点时对轨道的压力为F1=7N，Q向右运动，并恰好能到达圆弧轨道的最高点E，Q返回后与平板车相对静止时恰好在CD的中点。已知重力加速度g取10m/s2，sin53°=0.8，c0s53°=0.6。(计算结果可用分数表示)求：
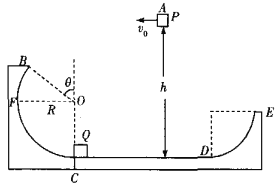
(1)滑块到达C点时的速度；
(2)若火药爆炸时释放的能量全部转化为机械能，求火药释放的化学能；
(3)Q与平板车间的动摩擦因数。
【答案】（1）14m/s（2）57.5J（3）1/3
【解析】
（1）P从A到B做平抛运动，在B点的速度方向与OB垂直，结合几何关系和动能定理求解滑块到达C点时的速度；（2）根据动量守恒定律以及能量关系求解火药释放的化学能；（3）Q到达E点返回后平板车相对静止时二者共速，对Q和平板车由动量守恒定律和能量关系求解Q与平板车间的动摩擦因数.
（1）P从A到B做平抛运动，在B点的速度方向与OB垂直，根据速度分解可得
解得t=0.8s
根据几何关系：
解得R=3m
设从A经B到C的速度为v，则由动能定理：
解得v=14m/s
（2）设PQ碰撞经火药爆炸后速度分别为v1和v2，p返回到F点的速度为v1′，则碰撞时有：
碰撞后P返回到F过程有：
在F点：
联立解得：v1=9m/s，v2=10m/s
根据能量守恒定律：
解得：E=57.5J
（3）Q到达E点返回后平板车相对静止时二者共速，对Q和平板车由动量守恒定律可得：
根据能量守恒定律：
联立解得
【题目】某实验小组利用如下器材测量某金属丝的电阻率：
A.电源(3V，内阻约为0.1Ω)
B.电流表(量程0.6A，内阻约为0.1Ω)
C.电流表(量程3A，内阻约为0.03Ω)
D.电压表(量程3V，内阻约为3kΩ)
E.滑动变阻器(1kΩ，0.3A)
F.滑动变阻器(20Ω，2A)
G.待测金属丝、螺旋测微器、米尺、开关和导线等
(1)实验的主要步骤如下：
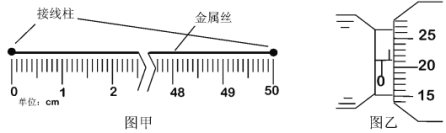
a.截取一段金属丝，拉直并固定在两端带有接线柱的米尺上，观察其接入长度在米尺上的示数如图甲所示，则读数为L=___________cm；
b.用螺旋测微器测出金属丝的直径，某次测量时示数如图乙所示，其读数为D=___________mm；
c.正确连接电路，合上开关；
d.改变滑动变阻器的位置，读出电压表和电流表的示数，记录如下表：
次数 | 1 | 2 | 3 | 4 | 5 |
U/V | 0.80 | 1.00 | 1.50 | 1.80 | 2.30 |
I/A | 0.18 | 0.22 | 0.34 | 0.42 | 0.52 |
e.断开开关，整理器材，结束实验操作。
(2)根据以上信息，你认为该小组选用的电流表是___________，滑动变阻器是___________(只填仪器前的代号)；请设计一个电路并使其尽可能测得更多的数据，据此把下列电路连接完整_______。
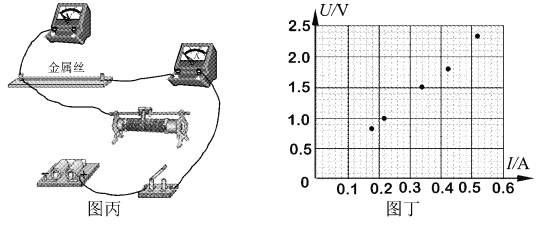
(3)该小组的测量数据已标在U-Ⅰ图上，据此可计算该金属丝的电阻值为___________Ω(保留两位有效数字)，根据电阻定律即可得到该金属丝电阻率。
