题目内容
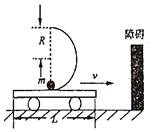
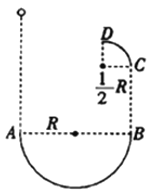
【题目】如图所示，半径为R的光滑半圆轨道固定在竖直面内，开口向上，两端点A、B连线水平，半径为R/2的四分之一光滑圆弧轨道也在竖直面内，C端在B点正上方，D端的切线水平。一个质量为m的小球从A点正上方由静止下落，从A点进入半圆轨道后从B点飞出再进入四分之一圆弧轨道，重力加速度为g。要使小球从D点飞出后刚好从A点进入轨道，则BC间的高度最大为（ ）
A. RB. 
C. 2RD. 
【答案】B
【解析】
小球从D点抛出刚好落在A点，做平抛运动的水平位移为
，BC间的高度越大，平抛运动的时间越长，做平抛运动的水平分速度越小，当小球在D点对轨道的压力恰好为零时，从D点抛出的速度最小。根据牛顿运动定律得：
，得：
。由平抛运动的规律得：
解得：
。设BC间的高度为
，则有：
，解得：
，故B正确。
练习册系列答案
相关题目
