题目内容
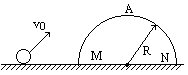
 如图所示,一光滑的半径为R的半圆形轨道固定在水平面上,与水平面相切于A点.一个质量为m的小球以某一速度冲上圆轨道时恰能通过最高点B,则小球从轨道口B飞出后的落地点C距A处多远?
如图所示,一光滑的半径为R的半圆形轨道固定在水平面上,与水平面相切于A点.一个质量为m的小球以某一速度冲上圆轨道时恰能通过最高点B,则小球从轨道口B飞出后的落地点C距A处多远?分析:当小球将要从轨道口飞出时,轨道的压力恰好为零,小球做圆周运动,只有重力提供向心力,因此求出这时小球的速度,小球以此速度做平抛运动,由B到C由平抛运动规律求C到A的距离.
解答:解:根据题意,在B点时,轨道压力为0,则:
mg=m
解得:
vB=
小球从B点做平抛运动,
竖直方向有:t=
=
,
水平方向有:s=vBt=
?
=2R
答:小球从轨道口B飞出后的落地点C距A点的距离为2R.
mg=m
| ||
| R |
解得:
vB=
| gR |
小球从B点做平抛运动,
竖直方向有:t=
|
|
水平方向有:s=vBt=
| gR |
|
答:小球从轨道口B飞出后的落地点C距A点的距离为2R.
点评:解答此题关键是分析小球的运动过程,明确小球分别在B的受力,选用牛顿第二定律求解B点速度,然后利用平抛运动规律可求小球落地点C到A的距离.

练习册系列答案
相关题目
(2011年北京四中一模)如图所示,表面光滑的半圆柱体固定在水平面上,小物块在拉力F作用下从B点沿圆弧缓慢上滑至A点,此过程中F始终沿圆弧的切线方向,则( )
| A.小物块受的支持力逐渐变大 |
| B.小物块受的支持力先变小后变大 |
| C.拉力F逐渐变小 |
| D.拉力F先变大后变小 |
 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( ) (2012?无锡二模)如图所示,在光滑的水平面上有一直角坐标系Oxy.现有一个质量m=O.lkg.带电荷量q=一2×10-4C的微粒,从y轴正半轴上的P1点以速度v0=0.6m/s垂直于y轴射入.已知在y>0的空间内有与y轴方向平行的匀强电场,在y<0的空间内存在方向与纸面垂直的匀强磁场.带电微粒从P1点射入电场后,经坐标(1.2,0)的P2点与x轴正方向成53°角射入y<0的空间,最后从y轴负半轴上的P3点垂直于y轴射出.(已知:sin53=0.8,cos53°=0.6)求:
(2012?无锡二模)如图所示,在光滑的水平面上有一直角坐标系Oxy.现有一个质量m=O.lkg.带电荷量q=一2×10-4C的微粒,从y轴正半轴上的P1点以速度v0=0.6m/s垂直于y轴射入.已知在y>0的空间内有与y轴方向平行的匀强电场,在y<0的空间内存在方向与纸面垂直的匀强磁场.带电微粒从P1点射入电场后,经坐标(1.2,0)的P2点与x轴正方向成53°角射入y<0的空间,最后从y轴负半轴上的P3点垂直于y轴射出.(已知:sin53=0.8,cos53°=0.6)求: