题目内容
6.一小球从离地高度为h的地方,以初速度v0水平抛出,阻力不计,求:(1)小球在空中飞行的时间;
(2)抛出点到落地点的距离;
(3)落地时速度为vt的大小.
分析 (1)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,由高度求出时间.
(2)根据初速度和时间求出水平位移,结合平行四边形定则求出抛出点到落地点的距离.
(3)由速度公式求出落地时竖直分速度,结合平行四边形定则求出落地时速度vt的大小.
解答 解:(1)由h=$\frac{1}{2}g{t}^{2}$得 t=$\sqrt{\frac{2h}{g}}$
(2)落地时水平位移大小 x=v0t=v0$\sqrt{\frac{2h}{g}}$
故抛出点到落地点的距离为 S=$\sqrt{{x}^{2}+{h}^{2}}$=$\sqrt{\frac{2h{v}_{0}^{2}}{g}+{h}^{2}}$
(3)落地时竖直分速度 vy=gt=$\sqrt{2gh}$
故落地时速度为 vt=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{{v}_{0}^{2}+2gh}$
答:
(1)小球在空中飞行的时间为$\sqrt{\frac{2h}{g}}$.
(2)抛出点到落地点的距离为$\sqrt{\frac{2h{v}_{0}^{2}}{g}+{h}^{2}}$.
(3)落地时速度大小为$\sqrt{{v}_{0}^{2}+2gh}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和平行四边形定则求解.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
16.关于经典力学,以下说法错误是( )
| A. | 经典力学的基础是牛顿运动定律 | |
| B. | 经典力学认为物体的体积跟物体的运动状态无关 | |
| C. | 经典力学认为时间是独立于物体及其运动而存在的 | |
| D. | 相对论和量子力学的出现,意味着经典力学失去了意义 |
17. 神舟九号飞船于2012年6月16日从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器成功进行了自动和手动两次对接.图为对接前天宫一号、神舟九号飞船围绕地球沿圆轨道运行的示意图,下列说法中正确的是( )
神舟九号飞船于2012年6月16日从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器成功进行了自动和手动两次对接.图为对接前天宫一号、神舟九号飞船围绕地球沿圆轨道运行的示意图,下列说法中正确的是( )
 神舟九号飞船于2012年6月16日从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器成功进行了自动和手动两次对接.图为对接前天宫一号、神舟九号飞船围绕地球沿圆轨道运行的示意图,下列说法中正确的是( )
神舟九号飞船于2012年6月16日从酒泉卫星发射中心发射升空,先后与天宫一号目标飞行器成功进行了自动和手动两次对接.图为对接前天宫一号、神舟九号飞船围绕地球沿圆轨道运行的示意图,下列说法中正确的是( )| A. | 天宫一号的速率大于神舟九号飞船的速率 | |
| B. | 天宫一号的加速度大于神舟九号飞船的加速度 | |
| C. | 天宫一号的周期大于神舟九号飞船的周期 | |
| D. | 天宫一号的机械能一定小于神舟九号飞船的机械能 |
14.牛顿以天体之间普遍存在着引力为依据,运用严密的逻辑推理,建立了万有引力定律.在牛顿创建万有引力定律的过程中,以下说法错误的是( )
| A. | 接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想 | |
| B. | 根据地球上一切物体都以相同加速度下落的事实,得出物体受地球的引力与其质量成正比,即F∝m的结论 | |
| C. | 根据F∝m和牛顿第三定律,分析了地、月间的引力关系,进而得出F∝m1、m2 | |
| D. | 根据大量实验数据得出了比例系数G的大小 |
1.如图所示,通电导线旁边同一平面有矩形线圈a则( )
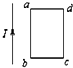

| A. | 若线圈向右平动,其中感应电流方向是a→b→c→d→a | |
| B. | 当线圈向导线靠近时,无感应电流产生 | |
| C. | 当线圈从图示位置以ab边为轴转动时,其中感应电流方向是a→b→c→d→a | |
| D. | 若线圈竖直向下平动,无感应电流产生 |
11.下列说法中正确的是( )
| A. | 居里夫人首先发现了天然放射现象 | |
| B. | 对天然放射现象的研究建立了原子的核式结构 | |
| C. | 压力和温度对放射性元素衰变的快慢没有任何影响 | |
| D. | 贝克勒耳通过对天然放射现象的研究,发现了质子和中子 |
18. 如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
 如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )| A. | 弹簧的弹性势能不断增大 | |
| B. | 小球的动能先增大后减小 | |
| C. | 小球的重力势能先增大后减小 | |
| D. | 小球的弹性势能和重力势能总和先增大后减小 |
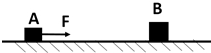 如图所示,光滑水平面上静止放置两物体A、B,mA=1kg,mB=2kg.现对A施加一个水平向右的恒力F=3N,经时间t=3s后撤去该力.A继续运动一段时间后,与B发生正碰,碰后A、B粘在一起以共同的速度向右运动.求:
如图所示,光滑水平面上静止放置两物体A、B,mA=1kg,mB=2kg.现对A施加一个水平向右的恒力F=3N,经时间t=3s后撤去该力.A继续运动一段时间后,与B发生正碰,碰后A、B粘在一起以共同的速度向右运动.求: