题目内容
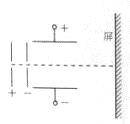
【题目】某匀强电场中的4个平行且等距的等势面如图中的虚线A、B、C、D所示,其中等势面C电势为零一电子仅在静电力作用下运动,经过等势面A、D时的动能分别为21eV和6eV,则下列说法正确的是( )
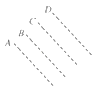
A. 电场方向垂直于等势面由D指向A
B. 等势面D的电势为﹣5V
C. 该电子可以到达电势为﹣12V的等势面
D. 若该电子运动到某位置时的电势能为8eV,则它的动能为3eV
【答案】BD
【解析】
根据动能定理,结合电势差等于电势之差,及能量守恒定律,及只有电场力做功,导致动能与电势能相互转化,从而即可一一求解。
A、因电子只在静电力的作用下运动,经过A、D等势面点的动能分别为21eV和6eV,根据动能定理,则有:![]() ,解得:
,解得:![]() ,A点的电势高,则电场线的方向垂直于等势面由A指向D,故A错误;
,A点的电势高,则电场线的方向垂直于等势面由A指向D,故A错误;
B、![]() ,可解得:
,可解得:![]() ,故B正确;
,故B正确;
C、因只有电场力做功,动能与电势能之和保持不变,当电子的速度为零时,由能量守恒定律,可知,![]() ,解得:φ=﹣10V,则该电子不可以到达电势为﹣12V的等势面,故C错误;
,解得:φ=﹣10V,则该电子不可以到达电势为﹣12V的等势面,故C错误;
D、同理,由能量守恒定律,可知,![]() ,解得:
,解得:![]() ,故D正确;
,故D正确;
故选:BD。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目