题目内容
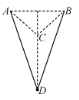
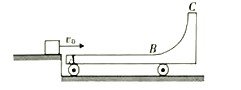
【题目】如图所示，在光滑的水平面上有一辆小车处于静止状态，小车的上表面左端AB部分是水平的轨道，右侧BC是一段光滑的
圆弧轨道，圆弧的底端恰好与AB段相切，小车质量M=8kg，现有一质量m=2kg的物块，以初速度
从A点冲上小车，并沿BC上滑，然后恰好沿轨道返回到A点，已知物块与水平面AB部分的动摩擦因数
，求：
（1）小物块返回到A点的速度大小；
（2）小车上平面AB的长度
；
（3）要使物块不从C点冲出，圆弧BC的半径R的最小值。
【答案】（1）2m/s（2）10cm（3）2m
【解析】（1）小物块和小车组成的系统在水平方向上的动量总是守恒，小物块恰好返回到A点，所以小物块返回到A点和小车的速度相同，设它们的共同速度为v，则有：
，
解得：
；
（2）小物块返回到A点时，小物块的动能减少，小车的动能增加，系统的内能增加，由能量守恒定律得：
，
解得：
。
（3）小物块在圆弧BC上运动到最高点C时，水平方向上的速度与小车相同，竖直方向上的速度为零，此时小物块刚好不冲出小车，圆弧半径最小，所以小物块和小车阻成的系统在水平方向上的动量守恒，有：
，
解得：
，
小物块在圆弧BC上运动到最高点C的过程中，小物块的动能减少，重力势能增加，小车的动能增加，由能量守恒定律得：
，
解得：
。
练习册系列答案
相关题目
