��Ŀ����
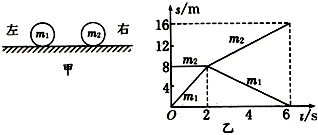
����Ŀ����ͼ��ʾ���ڱڹ⻬��ԲͲ�̶�������ԲͲ����������ֱ��������������ȵ�С��A��B�������ڱڷֱ�����ͼ��ʾ��ˮƽ����������Բ���˶�����֪��С���˶��Ĺ���뾶֮��rA��rB=2��1��ȡԲͲ����͵�CΪ�������ܲ����棬��A��B����
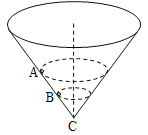
A. �˶�����֮��TA��TB=2��1
B. �ٶ�֮��vA��vB=![]() ��1
��1
C. ��е��֮��EA��EB=2��1
D. ���ļ��ٶ�֮��aA��aB=![]() ��1
��1
���𰸡�BC
�����������������С��������Բ���˶�����������֧�����ĺ��ṩ�����������ţ�ٵڶ������г������������ٶȡ����ٶȡ����ļ��ٶȵı���ʽ���Ӷ�������⣮
��֧��������ֱ�����ϵļн�Ϊ��������ţ�ٵڶ����ɵã� ![]() �����
�����![]() ����ΪA��BԲ�˶��İ뾶֮��Ϊ2��1������
����ΪA��BԲ�˶��İ뾶֮��Ϊ2��1������![]() ��
�� ![]() ��
�� ![]() ��AD����B��ȷ�������Ϸ�����֪
��AD����B��ȷ�������Ϸ�����֪![]() �����ݼ���֪ʶ��֪
�����ݼ���֪ʶ��֪![]() ����
����![]() �����ڻ�е��Ϊ���ܺ���������֮�ͣ���EA��EB=2��1��C��ȷ��
�����ڻ�е��Ϊ���ܺ���������֮�ͣ���EA��EB=2��1��C��ȷ��


��ϰ��ϵ�д�
 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
�����Ŀ